Предмет: Алгебра,
автор: Аноним
Помогите пожалуйста решить задачу
Приложения:
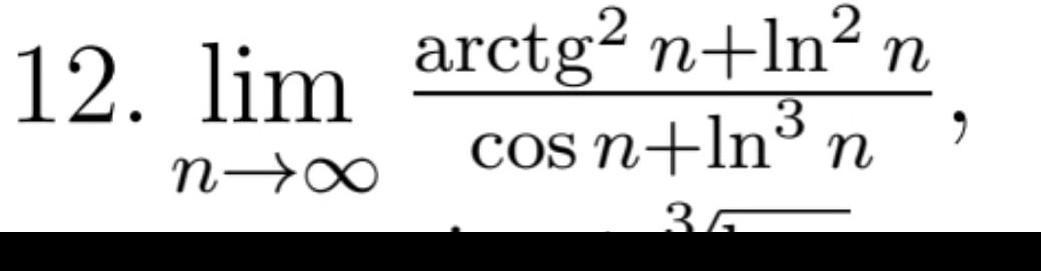
Ответы
Автор ответа:
1
Ответ:
0.
Объяснение:
Как известно, y=arctg x и y=cos x - функции ограниченные:
а y=ln x стремится к бесконечности, когда аргумент стремится к бесконечности. Поэтому
Мы воспользовались тем, что если ограниченную функцию разделить на бескогнечно большую, то получится функция бесконечно малая.
Похожие вопросы
Предмет: Алгебра,
автор: zenadubencuk953
Предмет: Алгебра,
автор: Sonia23008
Предмет: Математика,
автор: Nazarii15
Предмет: Английский язык,
автор: Аноним
Предмет: Литература,
автор: Apxip