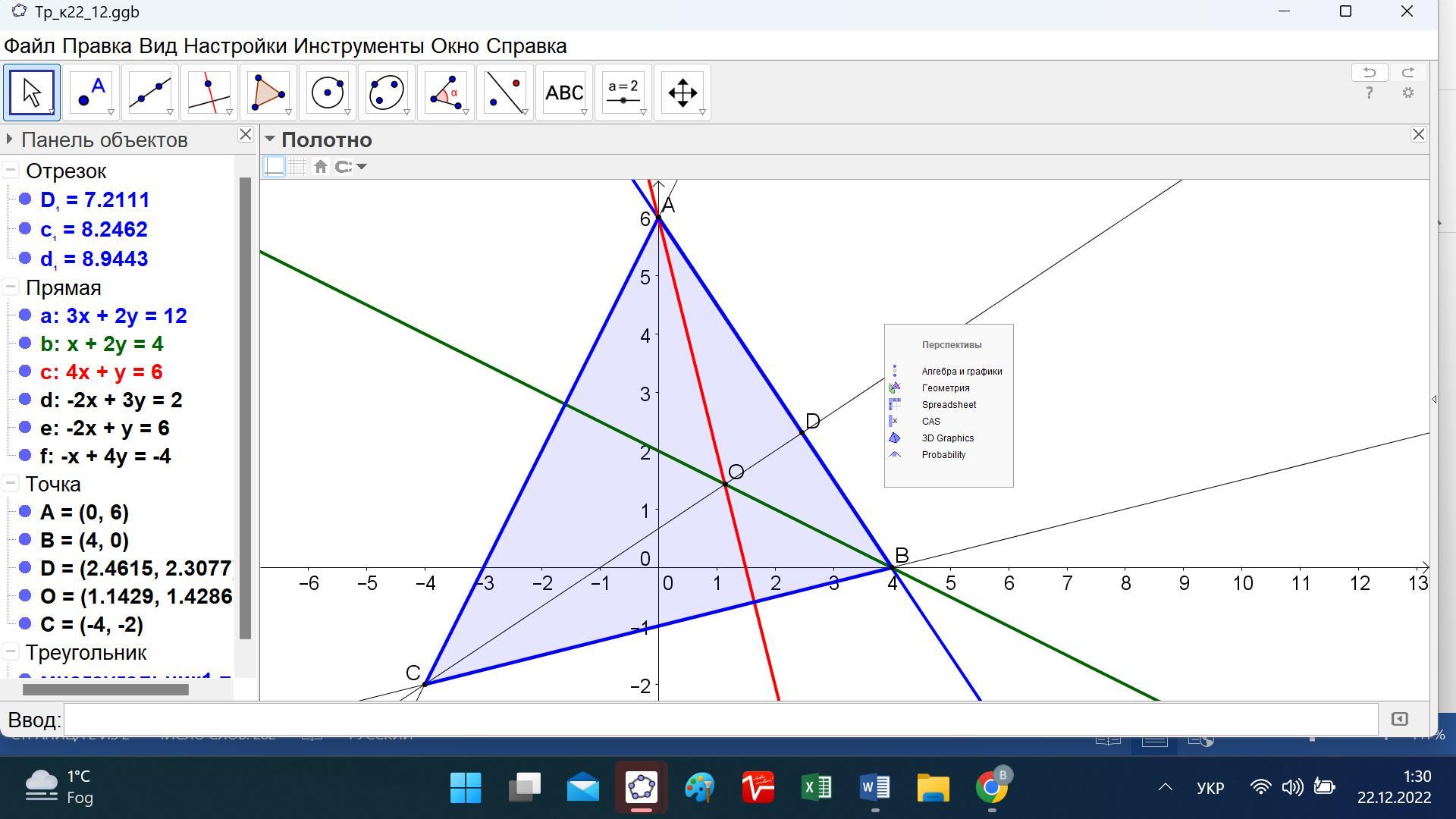
В треугольнике АВС дано уравнение стороны
AB: 3x+2y-12=0 и уравнения высот, опущенных из вершин A:x+2y=4 и B:4x+y=6. Найдите уравнение высоты, опущенной из
вершины С.
Ответы
Находим координаты точки О пересечения высот как систему уравнений.
x + 2y = 4 x + 2y = 4
4x + y = 6 (х(-2)) -8x - 2y=-12
-7х = -8 х = 8/7 ≈ 1,14286.
y = 6 – 4x = 6 – 4*(8/7) = (42 – 32)/7 = 10/7 ≈ 1,42857.
Точка О((8/7); (10/7)).
Далее используем свойство: высоты треугольника или их продолжения пересекаются в одной точке - ортоцентре треугольника.
Искомая высота из точки С проходит через точку О.
В уравнении СО как перпендикуляра к стороне АВ с уравнением 3x+2y-12=0 коэффициенты общего уравнения А и В меняются на В и (-А) или (-В) и А.
Получаем уравнение СО: 2x - 3y + С = 0. Для определения параметра С подставим координаты точки О((8/7); (10/7)).
2*(8/7) – 3*(10/7) + С = 0. Отсюда С = (30/7) – (16/7) = 14/7 = 2.
Ответ: уравнение высоты 2x - 3y + 2 = 0.