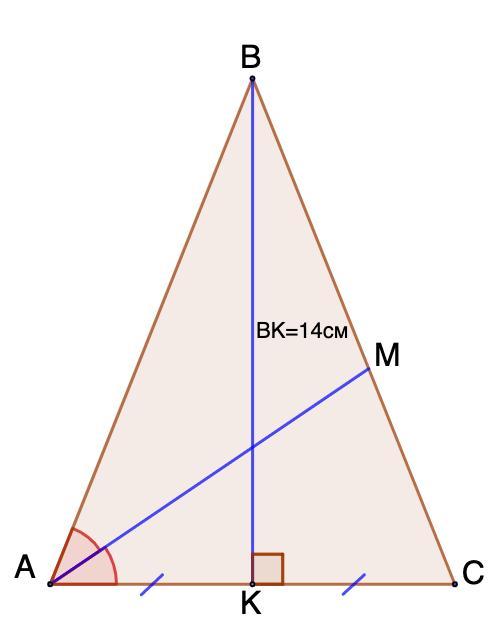
У рівнобедреному трикутнику АВС (АВ=ВС) медіана ВК дорівнює 14 см. Бісектриса кута А ділить сторону ВС у відношенні 5:4, рахуючи від вершини В. Знайдіть радіус вписаного кола трикутника АВС.
Ответы
Ответ:
Радиус вписанной окружности равен 4 см.
Объяснение:
В равнобедренном треугольнике АВС (АВ=ВС) медиана ВК равна 14 см. Биссектриса угла А делит сторону ВС в отношении 5:4, считая от вершины В. Найдите радиус вписанной окружности треугольника АВС.
Дано: ΔАВС - равнобедренный (АВ = ВС);
ВК - медиана; АМ - биссектриса;
ВМ : МС = 5 : 4
Найти: r - радиус вписанной окружности.
Решение:
Радиус вписанной окружности найдем по формуле:
,
где a, b, c - стороны треугольника, S - его площадь.
Рассмотрим ΔАВС - равнобедренный.
АМ - биссектриса.
ВМ : МС = 5 : 4
- Биссектриса угла треугольника делит противоположную сторону в отношении, равном отношению двух прилежащих сторон.
⇒ ВМ : МС = АВ : АС = 5 : 4
Пусть АВ = 5х см, тогда АС = 4х см.
ВК - медиана
⇒ АК = КС = 2х см.
- В равнобедренном треугольнике медиана, проведенная к основанию, является высотой и биссектрисой.
⇒ ВК - высота.
Рассмотрим ΔАВК - прямоугольный.
Теорема Пифагора:
- Квадрат гипотенузы равен сумме квадратов катетов.
⇒ АВ² = ВК² + АК²
25х² = 196 + 4х²
21х² = 196
Отрицательное значение не подходит по условию задачи.
⇒
Стороны треугольника равны:
(см)
(см)
Найдем периметр - сумму длин всех сторон.
(см)
Стороны нашли. Найдем площадь.
- Площадь треугольника равна половине произведения основания на высоту.
(см²)
Можем найти радиус вписанной окружности:
(см)
Радиус вписанной окружности равен 4 см.
#SPJ1