Question

помогите пожалуйста с объяснением! ​

Answer 1

Ответ:

Площадь фигуры, ограниченной линиями равна $\displaystyle 20\frac{5}{6}$  ед.²

Объяснение:

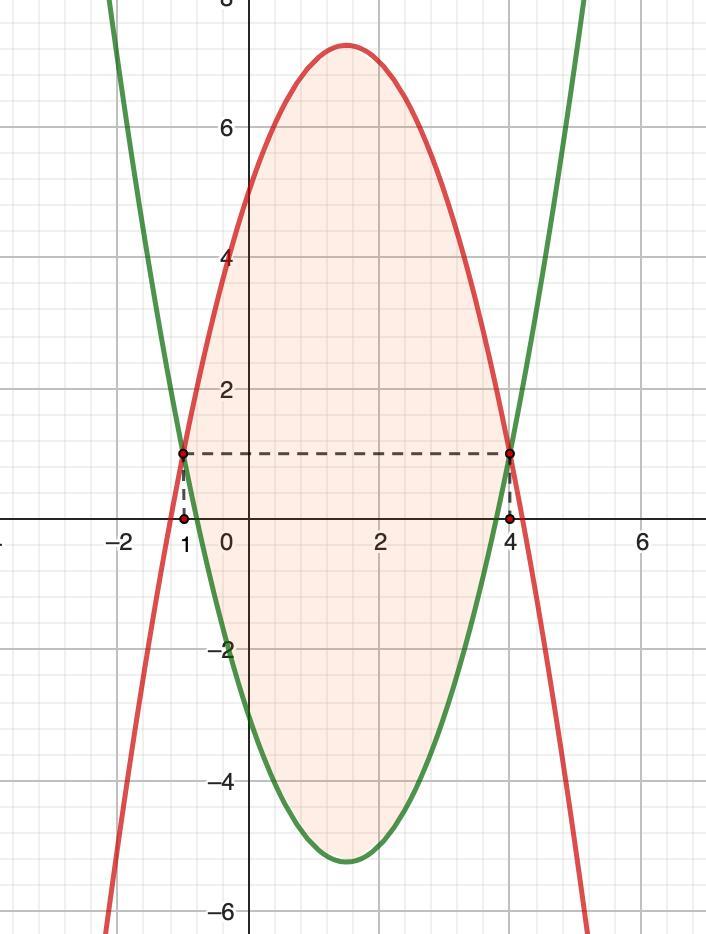
Вычисли площадь фигуры, ограниченной линиями.

y = x² - 3x - 3, y = 3x + 5 - х²

Найдем точки пересечения графиков.

Для этого решим систему:

$\displaystyle \left \{ {{y=x^2-3x-3} \atop {y=3x+5-x^2}} \right. \\\\x^2-3x-3=3x+5-x^2\\\\2x^2-6x-8=0\;\;\;|:2\\\\x^2-3x-4=0$

По теореме Виета:

х₁ = -1;   х₂ = 4

Это и будут пределы интегрирования.

Площадь фигуры найдем по формуле:

• $\boxed {\displaystyle\bf S=\int\limits^b_a {(f_2(x)-f_1(x))} \, dx}$

a = -1;  b = 4;  f₂(x) = y = 3x + 5 - х²;  f₁(x) = x² - 3x - 3

Подставим значения:

$\displaystyle S=\int\limits^{4}_{-1} {(3x+5-x^2-x^2+3x+3)} \, dx=\\\\\int\limits^{4}_{-1} {(-2x^2+6x+8)} \, dx=-\int\limits^{4}_{-1} {(x^2-3x-4)} \, dx$

Интеграл степенной функции:

$\boxed {\displaystyle\bf \int\limits {x^n} \, dx=\frac{x^{n+1}}{n+1}+C }$

$\displaystyle -\int\limits^{4}_{-1} {(x^2-3x-4)} \, dx=-\left(\frac{x^3}{3}-3\cdot \frac{x^2}{2}-4x\right)\bigg|^4_{-1}=\\ \\ =-\left(\left(\frac{4^3}{3}-3\cdot \frac{4^2}{2}-4\cdot4\right)-\left(\frac{(-1)^3}{3}-3\cdot \frac{(-1)^2}{2}-4\cdot (-1)\right)\right)=\\\\=-\left(\frac{64}{3}-24-16+\frac{1}{3}+ \frac{3}{2}-4\right)\right)=\frac{125}{6}=20\frac{5}{6}$

Площадь фигуры, ограниченной линиями равна $\displaystyle 20\frac{5}{6}$  ед.²