Question

Розв'язати нерівність:
(x - 6)(x + 3) ≤ 2 - 2x.

​

Answer 1

Ответ:

x ∈ [ -4; 5]

все числа от -4 до 5, включая -4 и 5.

Объяснение:

$(x - 6)(x + 3) \leqslant 2 - 2x$

1. Раскрываем скобки:

${x}^{2} + 3x - 6x - 18 \leqslant 2 - 2x \\ {x}^{2} - 3x - 18 \leqslant 2 - 2x$

2. Можно решить обычное квадратное уравнение относительно 0, а можно как я с помощью разложения многочлена на множители:

${x}^{2} - x - 20 \leqslant 0 \\ {x}^{2} - 5x + 4x - 20 \leqslant 0 \\ x(x - 5) + 4(x - 5) \leqslant 0 \\ (x + 4)(x - 5) \leqslant 0$

3.

Так как мы получаем целых 2 корня, то рациональнее было бы воспользоваться методом интервалов.

В прикреплённом файле я уже все написал.

Кратко расскажу про метод интервалов:

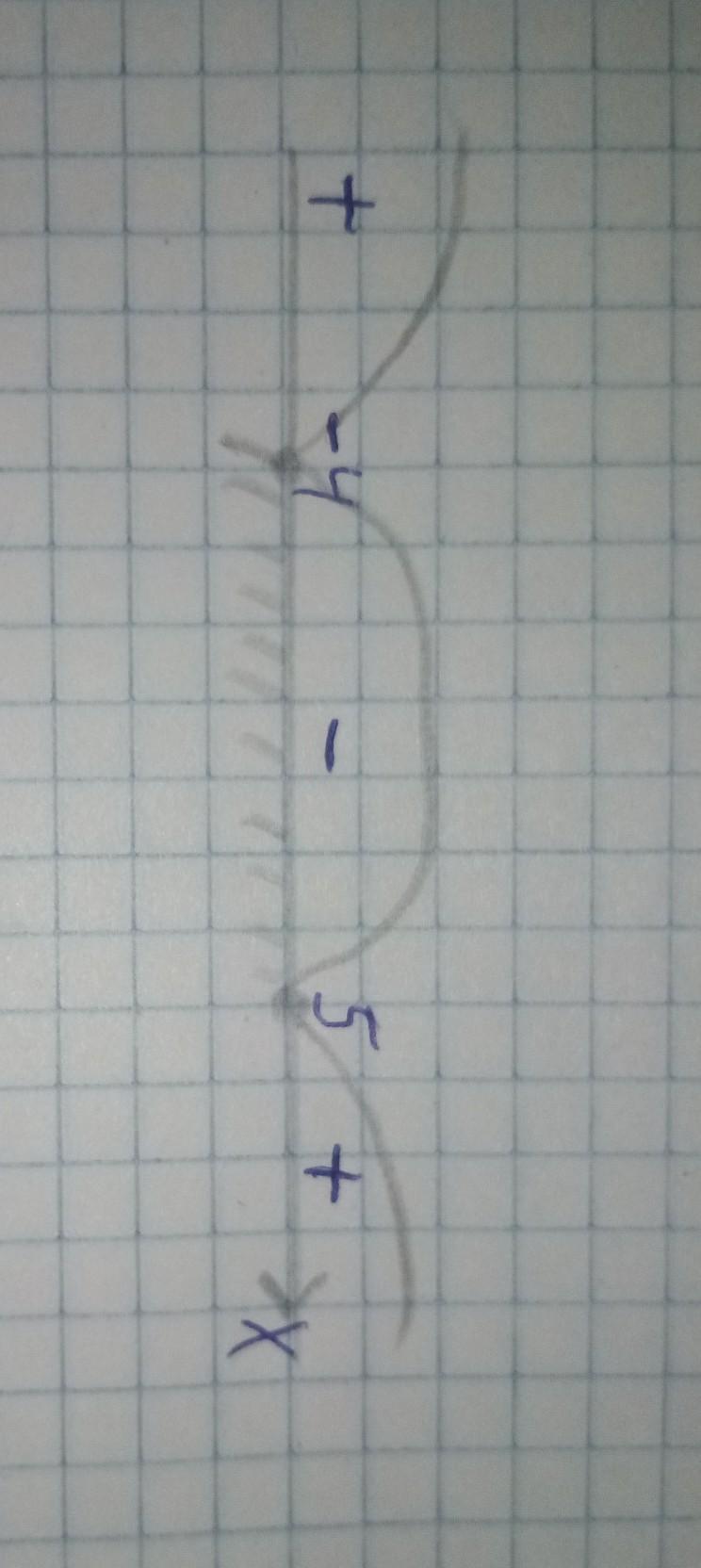
• Для начала, мы чертим координатную ось, на которой обозначаем все наши корни.
• Далее между каждыми интервалами мы вычисляем знаки. Если при подстановке корня из этого интервала значение нашего неравенства становится отрицательным, то ставим знак -. Если неравенство становится положительным, то +.
• И теперь просто смотрим на нашу координатную ось и находим приемлемые промежутки.

Так как знак неравенства показывает, что наше неравенство должно быть больше или равно 0, то значит нас интересуют интервалы со знаком -.

Это промежуток от - 4 до 5 включительно.

Математичечки данный промежуток обозначается таким образом:

x ∈ [ -4; 5]

Обратите внимание на скобки!

Так как знак неравенства не строгий, то числа -4 и 5 тоже являются корнями. Если бы наше уравнение имело вид:

$(x - 6)(x + 3) < 2 - 2x$

То это значит, что -4 и 5 не входят в промежуток, и обозначали мы это бы так:

x ∈ ( -4; 5)