Question

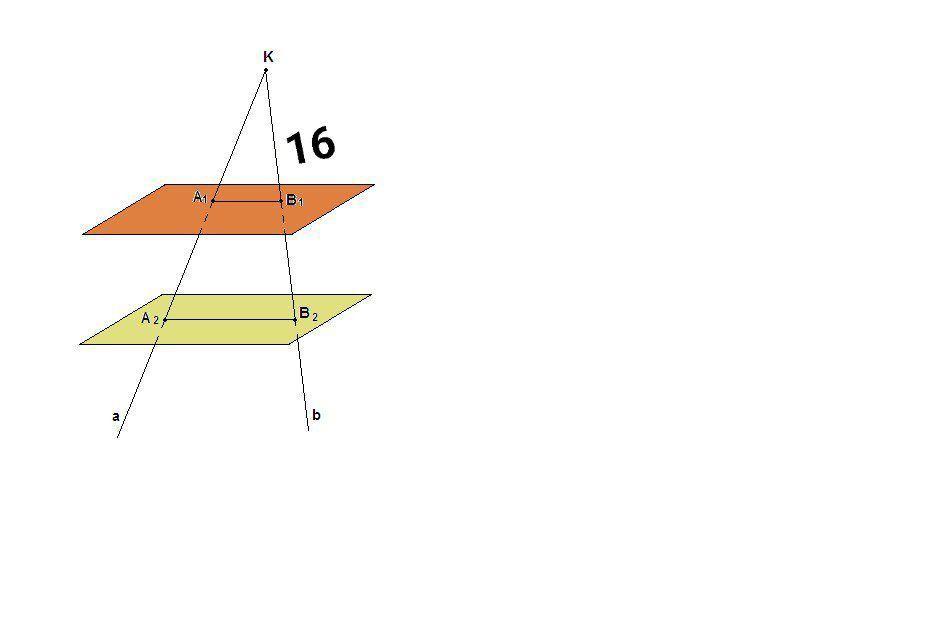
Через точку К, не лежащую между параллельными плоскостями (альфа) и (бета) проведены прямые а и b. Прямая a пересекает плоскости альфа и бета в точках А1 и А2 соответственно, b - в точках B1 и B2

Найдите B1B2,если A2B2:A1B1=18:8,KB1=16

Answer 1

Ответ:Пересекающиеся прямые а и b задают плоскость, которая пересекает параллельные плоскости по параллельным прямым. Значит А₁В₁ ║ А₂В₂. Тогда ∠КА₁В₁ = ∠КА₂В₂ как соответственные при пересечении параллельных прямых А₁В₁ ║ А₂В₂ секущей КА₂, угол при вершине К общий для треугольников КА₁В₁ и КА₂В₂, ⇒ Треугольники КА₁В₁ и КА₂В₂ подобны по двум углам. КВ₁ : КВ₂ = А₁В₁ : А₂В₂ 14 : КВ₂ = 3 : 4 КВ₂ = 14 · 4 /3 = 56/3 = 18 целых и 2/3 см

Объяснение: pon?