Предмет: Алгебра,
автор: tolya49
6.Решите уравнение
x²-7|x|+6=0.
Ответы
Автор ответа:
1
Ответ:
На фотографии,.................
Приложения:
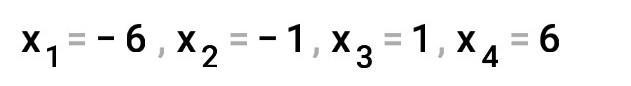
Автор ответа:
1
Чтобы решить это уравнение, нужно разделить его на две части, разложив уравнение по модулю |x|.
Если x≥0, то |x|=x, и уравнение имеет вид:
x²-7x+6=0
Это уравнение можно решить методом Виета:
x1,2= (7±√(49-24))/2 = 1,3
Если x<0, то |x|=-x, и уравнение имеет вид:
x²+7x+6=0
Это уравнение также можно решить методом Виета:
x1,2= (-7±√(49-24))/2 = -3,-1
Итого, решения уравнения x²-7|x|+6=0 равны x1=1, x2=3 (для x≥0) и x1=-3, x2=-1 (для x<0).
Уравнение x²-7|x|+6=0 не имеет решений в точках, где |x|=0.
x1=1, -1
x2=3, -3
Похожие вопросы
Предмет: Английский язык,
автор: saparbajnurmuhammed6
Предмет: Українська література,
автор: lukanenkodara66
Предмет: Биология,
автор: daniilchelovek71
Предмет: Другие предметы,
автор: linara795