Question

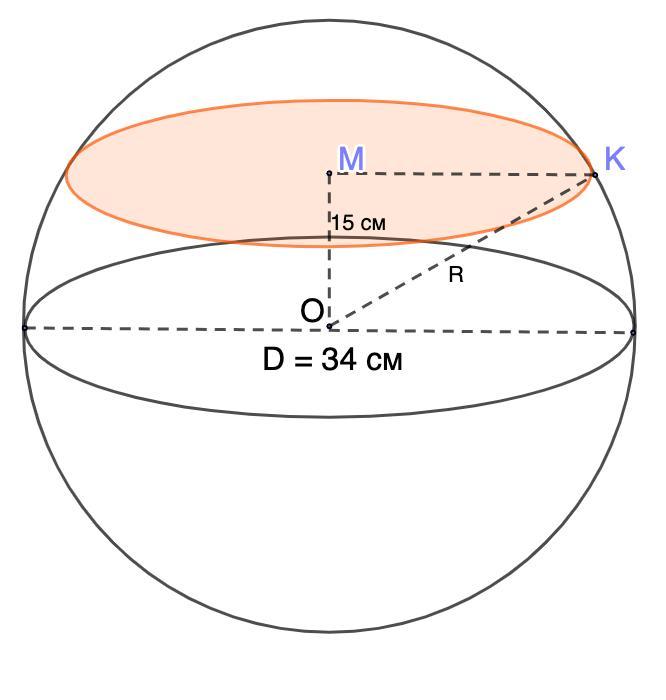
Діаметр кулі дорівнює 34 см. Знайдіть площу перерізу кулі площиною,
віддаленою від центра кулі на 15 см

Answer 1

Ответ:

Площадь сечения шара равна 64π см²

Объяснение:

Диаметр шара равен 34 см. Найдите площадь сечения шара плоскостью, удаленной от центра шара на 15 см.

Дано: шар;

D шара = 34 см;

ОМ = 15 см;

Найти: S сечения

Решение:

• Площадь круга равна:

        S = πR²

Сечение - круг радиуса МК.

Найдем радиус сечения.

Радиус равен половине диаметра.

⇒ ОК = R = D : 2 = 34 : 2 = 17 (см) - радиус шара.

Рассмотрим ΔОМК - прямоугольный.

ОК = 17 см; ОМ = 15 см;

По теореме Пифагора найдем МК:

МК² = ОК² - ОМ² = 289 - 225 = 64

МК = √64 = 8 (см)

Теперь можем найти площадь сечения:

S сечения = π · 8² = 64π (см²)

Площадь сечения шара равна 64π см²

#SPJ1