Question

помогите пожалуйста, если можно ! ​

Answer 1

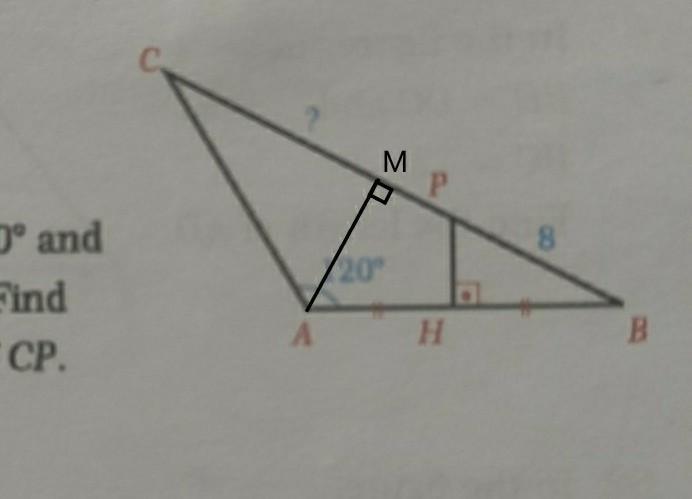
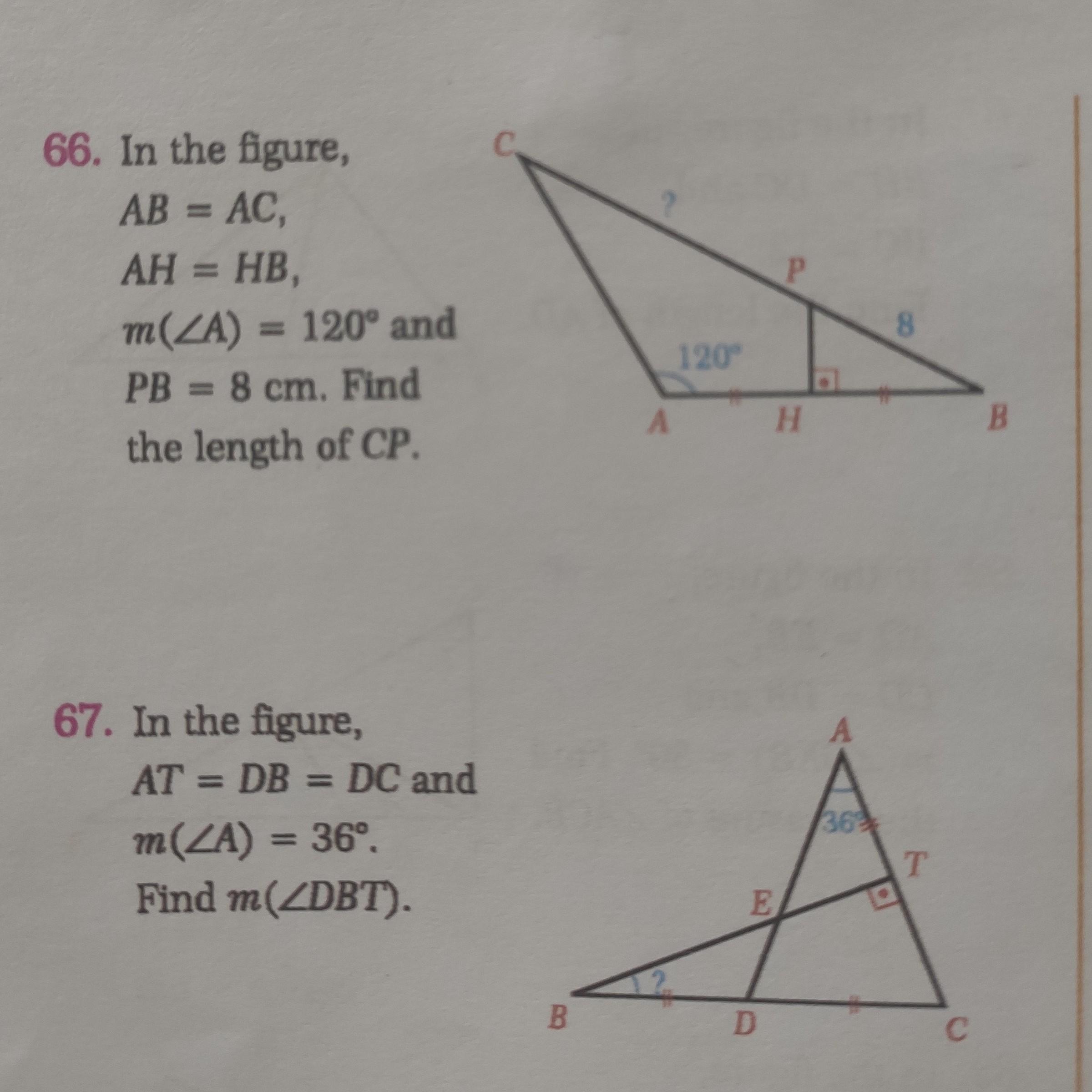
№66

∠C = ∠B = (180 - 120) / 2 = 30 °

1) PH = 8 / 2 = 4 см, так как PH лежит напротив угла 30° - ∠B

2) По теореме Пифагора - HB = √8² - 4² = 4√3 (8² - 4² под одним корнем пиши)

3) AB = AC = HB * 2 = 8√3

4) По теореме синусов имеем пропорцию:

CB / sin ∠A = AC / sin ∠B

x / 0.866 = 8√3 / 0.5
CB = 0.866 * 8√3 / 0.5 ≈ 24 см

CP = 24 - 8 = 16 см

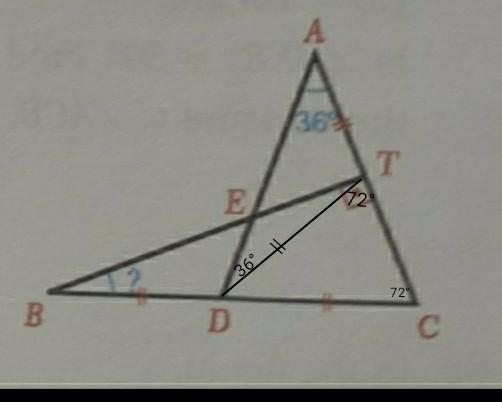
№67

∠AET = 90 - 36 = 54°

∠AET = ∠BED = 54 °, как вертикальный

∠TED = 180 - 54 = 126° как совместный

Как дальше, я пока что не знаю, надумаю, отредактирую и напишу

Answer 2

Ответ:

66) СР=16

67) ∠В=18°

Объяснение:

66)

∆АВС- равнобедренный треугольник, по условию АВ=АС.

В равнобедренном треугольнике углы при основании равны.

∠В=∠С.

Сумма углов в треугольнике равна 180°

∠В=(180°-∠САВ)/2=(180°-120°)/2=30°.

∆РНВ- прямоугольный треугольник.

РН- катет против угла ∠В=30°;

РН=РВ/2=8/2=4.

По теореме Пифагора:

НВ=√(РВ²-РН²)=√(8²-4²)=4√3.

АВ=2*НВ=2*4√3=8√3.

Проведем высоту АМ- высота, медиана и биссектриса, равнобедренного треугольника ∆АВС.

∆АМВ- прямоугольный треугольник.

АМ- катет против угла ∠В=30°;

АМ=АВ/2=8√3/2=4√3.

По теореме Пифагора:

МВ=√(АВ²-АМ²)=√((8√3)²-(4√3)²)=

=√(192-48)=√144=12.

СМ=МВ, АМ- медиана.

СВ=2*МВ=2*12=24.

СР=СВ-ВР=24-8=16.

_________________

67)

DT- медиана прямоугольного треугольника ∆ВТС.

Медиана проведенная к гипотенузе равна половине гипотенузы.

DT=BD=DC; (радиус описанной окружности)

∆АТD- равнобедренный треугольник. DT=AT.

В равнобедренном треугольнике углы при основании равны:

∠DAT=∠ADT=36°;

∠DTC=∠DAT+∠ADT; внешний угол треугольника ∆АТD.

∠DTC=36°+36°=72°;

∆DTC- равнобедренный треугольник DT=DC.

Углы при основании равны

∠DTC=∠DCT=72° (∠DCT=∠C=72°)

∆BTC- прямоугольный треугольник, ∠ВТС=90°;.

Сумма острых углов в прямоугольном треугольнике равна 90°: ∠В+∠С=90°;

∠В=90°-∠С=90°-72°=18°

_________