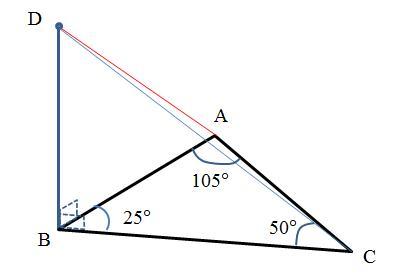
У трикутнику АВС ∟А=105°, ∟В=25°. Із точки В проведено перпендикуляр ВД до площини трикутника АВС. Розташуйте відрізки ДА, ДВ, ДС у порядку зростання їхніх довжин. (Зробити рисунок і дати пояснення).
Ответы
Ответ:
DB, DA, DC
Объяснение:
Перевод и исправление: В треугольнике АВС ∠А=105°, ∠В=25°. Из точки D проведен перпендикуляр BD к плоскости треугольника АВС. Разместите отрезки DA, DB, DC в порядке возрастания их длин. (Сделать рисунок и дать объяснение).
Нужно знать:
1) В треугольнике против большей стороны находится больший угол; против меньшего угла находится меньшая сторона.
2) Теорема Пифагора: В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
3) Перпендикуляр, опущенный из точки на плоскость, короче всякой наклонной, проведенной из той же точки к той же плоскости.
Решение. См. рисунок.
На основе пункта 3) заключаем: отрезок DB короче наклонной DA и наклонной DC: DB < DA, DB < DC.
На основе пункта 1) заключаем: В треугольнике ABC сторона BA короче чем сторона BC: BA < BC.
По теореме Пифагора
в ΔDBA: DA² = DB² + BA²,
в ΔDBC: DC² = DB² + BC².
Так как BA < BC, то
DA² = DB² + BA² < DB² + BC² = DC²,
то есть DA < DC.
#SPJ1