Question

В правильной пирамиде DABC на ребрах AB и DC взяты точки М и Р соответственно так, что AM : AB=DP: DC = 1:3. Постройте сечение пирамиды плоскостью, проходящей через точки М и Р параллельно ребру АС. Найдите площадь построенного сечения, если DA = AB = 3​

Answer 1

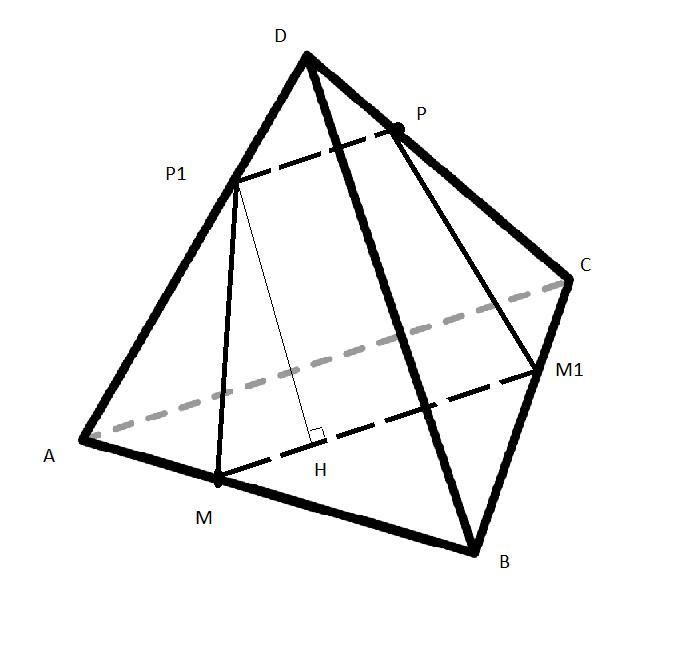
ММ1||AC||PP1, тогда в сечении трапеция

Через подобин треугольников находятся основания 1 и 2..

найду боковую сторону МР1 по т косинусов

АР1=2/3*AD=2

AM=1/3*AB=1

MP1^2=2^2+1^2-2*2*1*cos60=3

тогда по Пифагору найду высоту трапеции P1H

P1H^2=MP1^2-MN^2=3-(1/2)^2=2 3/4=11/4

P1H=√11/2

S=(2+1)/2*√11/2=0.75√11