Предмет: Алгебра,
автор: MirosaAkage
Ответ нужен срочно!
При каких значениях переменной имеет смысл выражение:
(5x)/(sqrt(3x - 7)) + 2/(x ^ 2 - 16) + sqrt(6 - x)
Приложения:
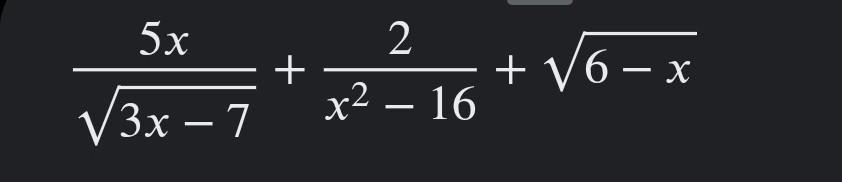
Ответы
Автор ответа:
2
1) Подкоренное выражение корня чётной степени должно быть неотрицательным , то есть ≥ 0 , но если этот корень в знаменателе , то подкоренное выражение должно быть строго больше нуля , так как на ноль делить нельзя .
2) Знаменатель дроби не должен равняться нулю .
Значит , для того , чтобы выражение имело смысл надо , чтобы одновременно выполнялись три условия :
MirosaAkage:
можете прикрепить фото пожалуйста?
Похожие вопросы
Предмет: Геометрия,
автор: madelinepersh
Предмет: Музыка,
автор: lukyanova201207
Предмет: Литература,
автор: traingle283
Предмет: Математика,
автор: karinamaslova12345
Предмет: Английский язык,
автор: znmxcnxmzc