Question

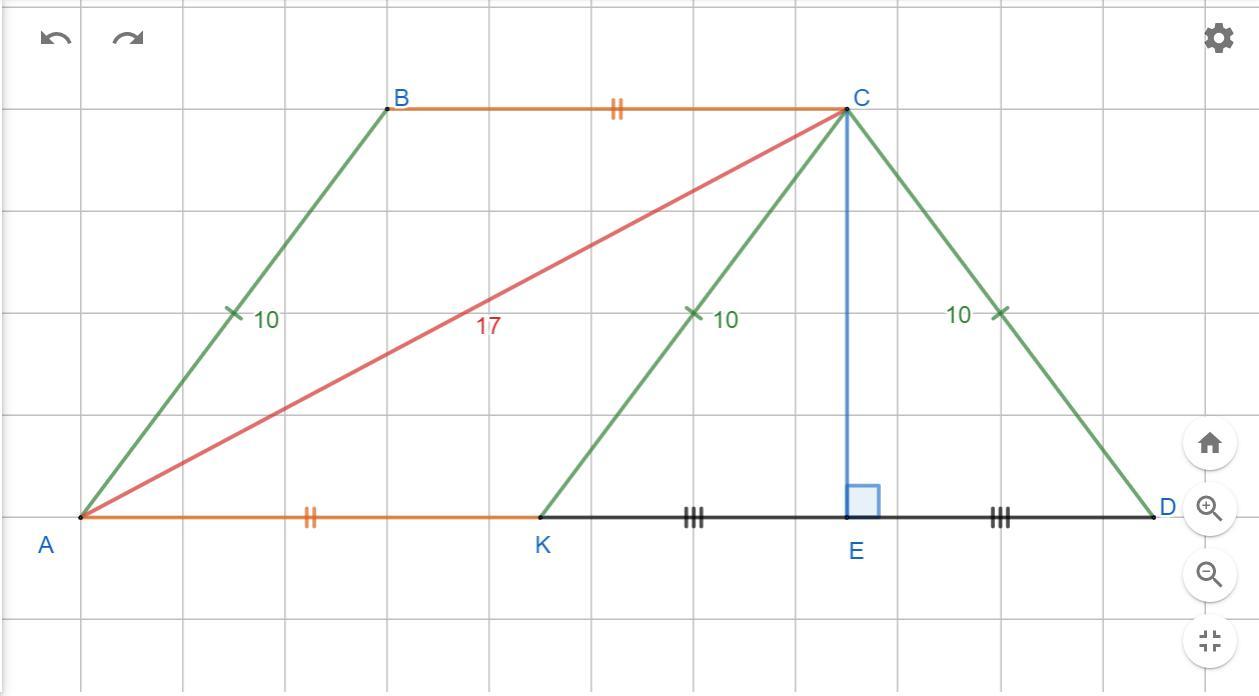
ABCD-трапеция, AB=CD=10, CK||AB, KD=12, AC=17. Найдите Sabcd​

Answer 1

Ответ:  Площадь трапеции равна  120 (ед)²

Пошаговое объяснение:

Дано :

ABCD - трапеция

AB = CD = 10

CK ║ AB ,   KD = 12 ,  AC = 17

$S _{ABCD}=?$

Чтобы найти площадь трапеции , нам нужно знать величину ее высоты ,  и двух противоположных оснований

Находим высоту трапеции (CE)

Поскольку нам дана трапеция ,  то противоположные стороны          BC ║ AC   т.к  AK является частью основания  AD  ,  то  BC ║ AK , и из условия  нам известно  CK ║ AB  ,  таким образом  четырехугольник  ABCK является параллелограммом , а из этого вытекает  что  :

BC = AK

CK = AB = 10  ⇒ ΔKDC  - равнобедренный

И т.к   ΔKDC  - равнобедренный  ,  то  высота  CE  будет  являться и биссектрисой и медианой  ,  и  она разделит  основание KD  на два равных отрезка  KE = ED = 12/2 = 6  

По теореме Пифагора , найдет высоту  CE

CE² + ED ²= CD²

CE²  + 6²  = 10²

CE  = 8

Находим  основания трапеции (BC,AD)

Рассмотрим  прямоугольный ΔACE ,  с помощью теоремы Пифагора найдем AE

AE² + CE² = AC²

AE² + 8² = 17²

AE² =  289 - 64

AE² = 225

AE = 15  

Теперь найдем AK

А как мы знаем :
AE = AK + KE    

AK +  6 =  15

BC = AK = 9  (меньшее основание)

А большее основание равно :

AD = AK + KD = 9 + 12 = 21

Находим площадь трапеции

$S = \dfrac{BC + AD}{2}\cdot CE =\dfrac{21 + 9 }{2}\cdot 8 = 15\cdot 8 = 120$  (ед)²

#SPJ1