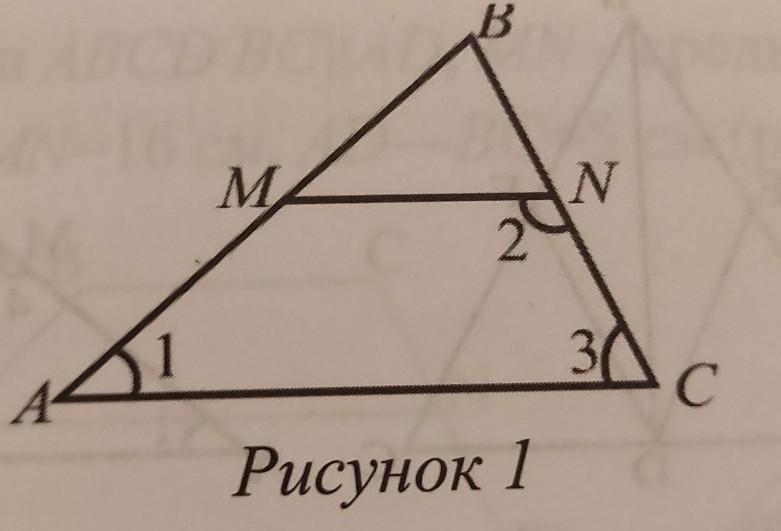
В треугольнике ABC, MN является средней линией и угол 3 ÷ угол 2 = 1:2. Найдите сумму ВС+АС, если угол 1 = 30°, BN = 4 см.
рисунок 1
Ответы
Відповідь:
Покрокове пояснення:
В трикутнику ABC, якщо MN є середньою лінією і кут 3 ділиться на кут 2 у відношенні 1:2, то це означає, що кут 3 є подвійним кутом 2. Тобто, кут 3 = 2 * кут 2.
Якщо кут 1 = 30°, то кут 2 = 60° і кут 3 = 120°. Оскільки трикутник є рівнобедреним, то кут 2 і кут 3 сумуються до 180°. Це означає, що кут 1 також дорівнює 180° - 30° - 60° = 90°.
Таким чином, трикутник ABC є прямокутним із вершиною А. Отже, ВС і АС - це катети цього трикутника. Наразі ми знаємо довжину одного з них (BN = 4 см), тому ми можемо використати теорему Піфагора, щоб знайти довжину іншого катета.
Теорема Піфагора говорить, що в прямокутному трикутнику квадрат гіпотенузи дорівнює сумі квадратів катетів. Тому:
АС^2 + ВС^2 = BN^2
АС^2 = BN^2 - ВС^2
АС = sqrt(BN^2 - ВС^2)