Предмет: Информатика,
автор: dfilatova25
Олимпийская задача по информатике
В Школу Нечародейства и Неволшебства прибыло N новых учеников. По прибытии их имена записали в список и пронумеровали неповторяющимися натуральными числами от 1 до N в порядке возрастания номеров.
В Школе Нечародейства и Неволшебства есть всего два класса - класс нечародеев и класс неволшебников. Распределяют учеников по классам тоже совершенно немагическим образом: первых S учеников из списка отправляют в класс нечародеев, следующих S учеников – в класс неволшебников, следующих S учеников – снова в класс нечародеев и так далее, пока все ученики не будут распределены по классам. В последней группе учеников может оказаться менее чем S учеников, но тем не менее и они будут определены в соответствующий по очереди класс.
Среди прибывших учеников есть двое друзей: Жора и Рома. Известно, что Жора записан в списке под номером X, а Рома – под номером Y. Определите, попадут ли друзья в один класс или в разные.
Входные данные
На вход программе подаётся четыре натуральных числа N, S, X, Y (2≤N≤109, 1≤S,X,Y≤N, X≠Y). Каждое число задаётся в отдельной строке.
Выходные данные
Выведите «YES», если Жора и Рома окажутся в одном классе, и «NO» в противном случае.
Приложения:
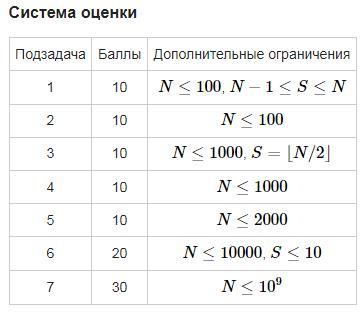
Ответы
Автор ответа:
0
Ответ: Двоечник(ца) Это олимпиада онлайн, а не списывание онлайн. Увидим такое же решение как ниже в комментариях ниже ? (или выше ?) - аннулируем работу.
Объяснение: Это кстати вражеская платформа.
Похожие вопросы
Предмет: Українська мова,
автор: orosanastasia40
Предмет: Геометрия,
автор: vika4887
Предмет: Математика,
автор: fjjfjdidjdj
Предмет: Информатика,
автор: ChimeraDa
Предмет: Алгебра,
автор: Аноним