Question

Площа бічної поверхні конуса дорівнює 48. Знайдіть площу основи конуса, якщо твірна утворює з площиною основи кут 60°.​

Answer 1

Ответ:

Площадь основания равна 24 ед.²

Объяснение:

Площадь боковой поверхности конуса равна 48. Найдите площадь основания конуса, если образующая образует с плоскостью основания угол 60°.​

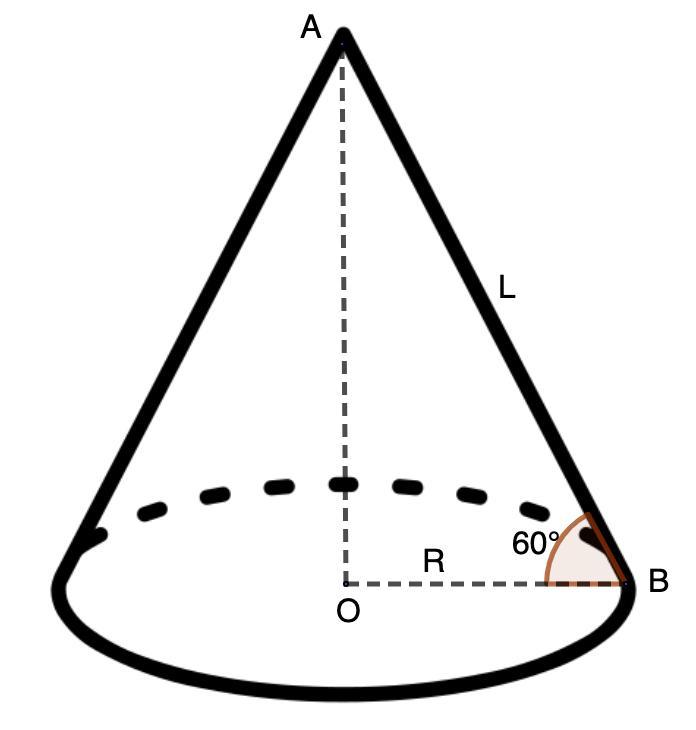
Дано: конус;

Sбок.= 48;

∠АВО = 60°

Найти: Sосн. конуса.

Решение:

• Площадь боковой поверхности конуса:
• Sбок. = πRL, где L - образующая, R - радиус основания конуса.

• Площадь основания: Sосн. = πR²

Рассмотрим ΔОАВ - прямоугольный.

• Сумма острых углов прямоугольного треугольника равна 90°.

⇒ ∠ОАВ = 90° - 60° = 30°

• Катет, лежащий против угла в 30°, равен половине гипотенузы.

⇒ ОВ = АВ : 2

ОВ = R;   AB = L;  

⇒ L = 2R

Площадь боковой поверхности равна:

48 = πR · 2R

$\displaystyle R^2=\frac{48}{2\pi } =\frac{24}{\pi }$

Тогда площадь основания равна:

$\displaystyle S_{OCH}=\pi \cdot\frac{24}{\pi } =24$

Площадь основания равна 24 ед.²

#SPJ1