Предмет: Алгебра,
автор: ivancomdee7
Помогите пожалуйста, задание на фотографии
Приложения:

Ответы
Автор ответа:
1
Ответ:
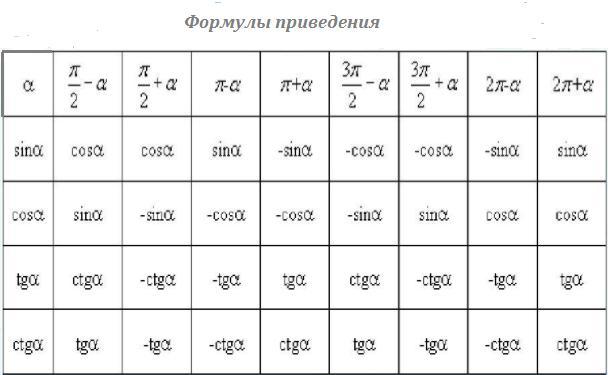
1) Применим формулы приведения и учтём периодичность тригонoметрических функций .
Формула косинуса двойного угла:
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: damirnurlybek5959
Предмет: Химия,
автор: nikitanikit988
Предмет: Қазақ тiлi,
автор: grisajvaleria
Предмет: Геометрия,
автор: abubakirabdulla5555