Довжина гіпотенузи прямокутного трикутника дорівнює 40 см. Вершини трикутника знаходяться на сфері. Визнач відстань площини трикутника від центру сфери, якщо радіус сфери дорівнює 25 см.
Ответы
Ответ:
О1О- 15см
Пошаговое объяснение:
Для удобства решении задачи в низу будут прикреплены пронумерованные три фото.
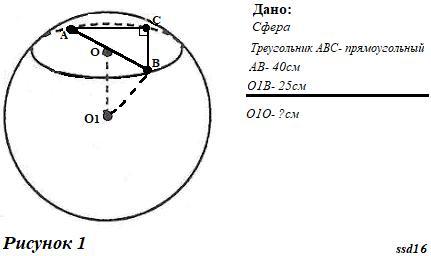
На рисунке 1 приведен общий вид условия задачи.
Что бы найти расстояние плоскости треугольника от центра сферы, проведем отрезок О1О(то что надо найти за условием задачи). О1О ⊥ плоскости ΔАВС.
Для решения задачи будем использовать рисунки 2 и 3.
1.Рассмотрим рисунок 2. У нас дан прямоугольный Δ АВС.
АВ- 40см
∠С- 90°
!Важное правило для решения задачи: Если вокруг прямоугольного треугольника описана окружность, то гипотенуза является диаметром такой окружности, а ее центр делит гипотенузу пополам.
↓
Диаметр круга с центром в точке О равен гипотенузе прямоугольного Δ АВС. → d=AB=40см (d- диаметр).
↓
↓
AO=OB=R=20 см
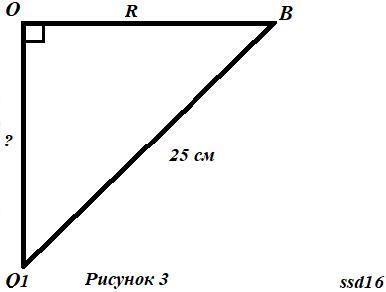
2. Перейдем к рисунку 3. Нам дан прямоугольный ΔO1OB
O1B- радиус сферы 25см.
ОВ- радиус круга с центром в точке О, 20см.
О1О- расстояние плоскости треугольника от центра сферы ?см.
∠О- 90°.
!Важное правило для решения задачи:
Теорема Пифагора: В прямоугольном треугольнике квадрат гипотенузы равен суме квадратов катетов.
ОВ- катет.
О1О- катет.
О1В- гипотенуза.
↓
Чтоб найти О1О, посчитаем корень разницы квадратов гипотенузы О1В и катета ОВ.
О1О- 15см