Предмет: Геометрия,
автор: ivankaromaniuk43
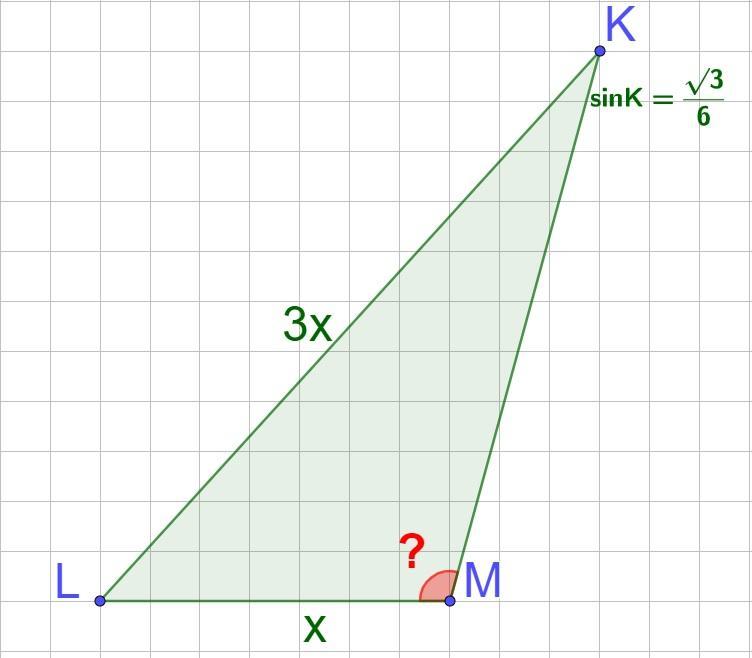
СРОЧНО! ПОМОГИТЕ ПОЖАЛУЙСТА!!! У трикутнику KLM KL=3LM, sin K = √3:6. Якому значенню може дорівнювати кут M?
Ответы
Автор ответа:
2
Ответ:
Кут М може дорівнювати 60° або 120°
Объяснение:
У трикутнику KLM KL=3LM, sin K = √3:6. Якому значенню може дорівнювати кут M?
Теорема синусів
Сторони трикутника пропорційні синусам протилежних кутів:
де a, b, c - сторони трикутника, протилежні кутам А, В і С відповідно.
Розв'язання:
За теоремою синусів маємо:
Нехай LM=х, тоді KL=3LM=3х.
Отже:
Цьому значенню сиинуса відповідає два кути: 60° і 120°
Відповідь: Кут М може дорівнювати 60° або 120°
#SPJ1
Приложения:
Похожие вопросы
Предмет: Информатика,
автор: anastasia7868
Предмет: Алгебра,
автор: karinka3761wert
Предмет: Литература,
автор: fguygko
Предмет: Английский язык,
автор: kozerogiklove
Предмет: Информатика,
автор: sartaevaekaterina80