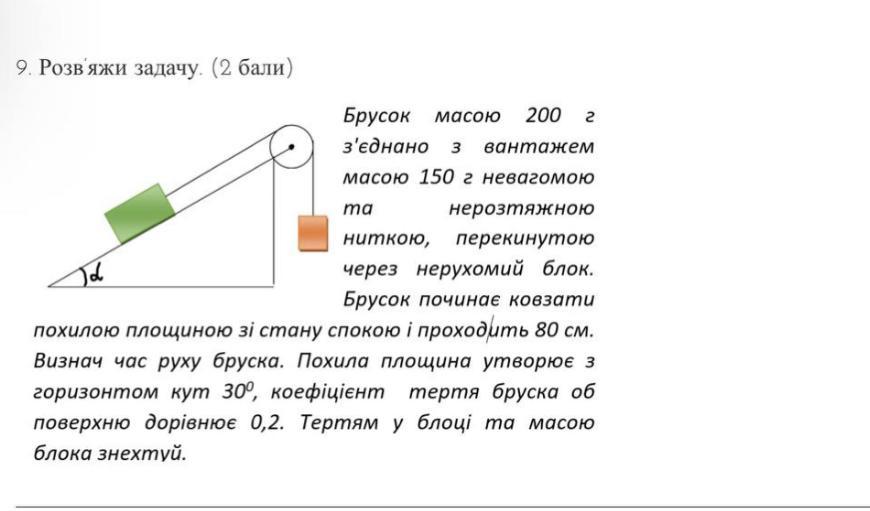
Брусок масою 200 г
з'єднано з вантажем
масою 150 г невагомою
нерозмяжною
ниткою, перекинутою
через нерухомий блок.
Брусок починає ковзати
похилою площиною зі стану спокою і проходить 80 см.
Визнач час руху бруска. Похила площина утворює з
горизонтом кут 30°, коефіцієнт тертя бруска об
поверхню дорівнює 0,2. Тертям у блоці та масою блоку знехтуй
Даю 50 баллов!!!
Ответы
Відповідь:
Пояснення:
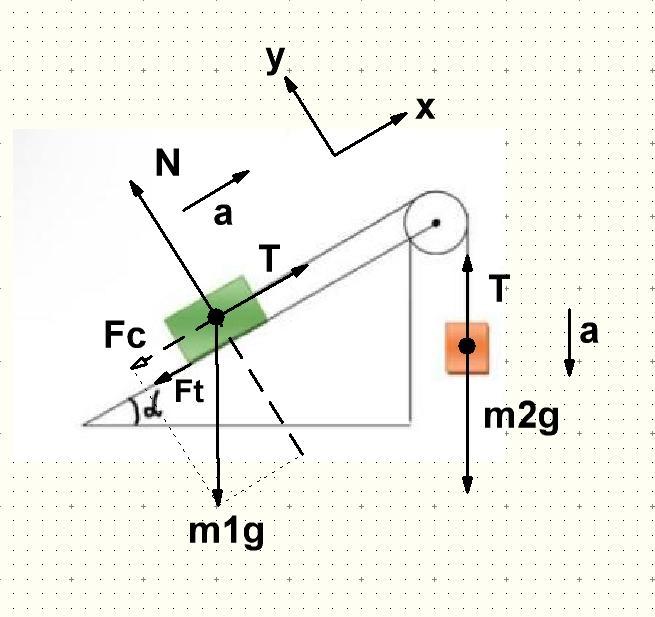
спочатку з'ясуєм, в якому напрямку може рухатись система
брусок масою 200 г лежить на похилій площині
сила тяжіння розкладається на 2 складові
вздовж площини та поперек.
та складова що вздовж площини і направлена донизу то є скочувальна сила. якщо вона більша за вагу тягарця 2 то система можливо буде скочуватись наліво
ми бачимо що
Fc = m₁*g*sin(30) = 0,2*10*0,5 = 1 Н
m₂g = 0,15*10 = 1,5 Н - сила тяжіння другого тягарця більша ніж скочувальна сила, отже рух бруска можливий тільки зліва направо, а тягарця зверху донизу.
різниця сил дорівнює 1,5 - 1 = 0,5 Н
завдяки цьому система має рухатись
вага бруска m₁*g*соз(30) = N = 0,2*10*0,866 = 1,732 Н
максимальна сила терття Ft = N*μ = 1,732*0,2 = 0,3464 Н - не перевищує 0,5 Н. це означає що система дійсно буде рухатись.
якби максимальна сила тертя перевищила різницю сил 0,5 Н то тіла б не ворушились.
ми зясували напрямок руху, тепер складем рівняння і знайдем прискорення
для бруска
сила натягу нитки тягне в один бік, скочуюча сила і сила тертя в інший, прискорення в бік сили натягу нитки Т
Т-m₁g*sin(30)-m₁g*cos(30)*μ=m₁a
для тягарця
сила тяжіння в один бік, сила натяжіння в інший. рух відбувається в напрямку сили тяжіння
m₂g-T=m₂a
маєм 2 рівняння. додамо їх одне до одного щоб скоротилось Т.
вирахуєм прискорення
Т-m₁g*sin(30)-m₁g*cos(30)*μ=m₁a
m₂g-T=m₂a
m₂g-m₁g*sin(30)-m₁g*cos(30)*μ = m₁a+m₂a = (m₁+m₂)*а
а = (m₂g-m₁g*sin(30)-m₁g*cos(30)*μ) / (m₁+m₂)
а = (0,15*10-0,2*10*0,5-0,2*10*0,866*0,2) / (0,2+0,15) ≈ 0,44 м/с²
тепер згадаєм формулу рівноприскоренного руху
S=a*t²/2
звідки t = √(2S/a) = корень(2*0,8/0,44) ≈ 1,9 сек - це відповідь