Question

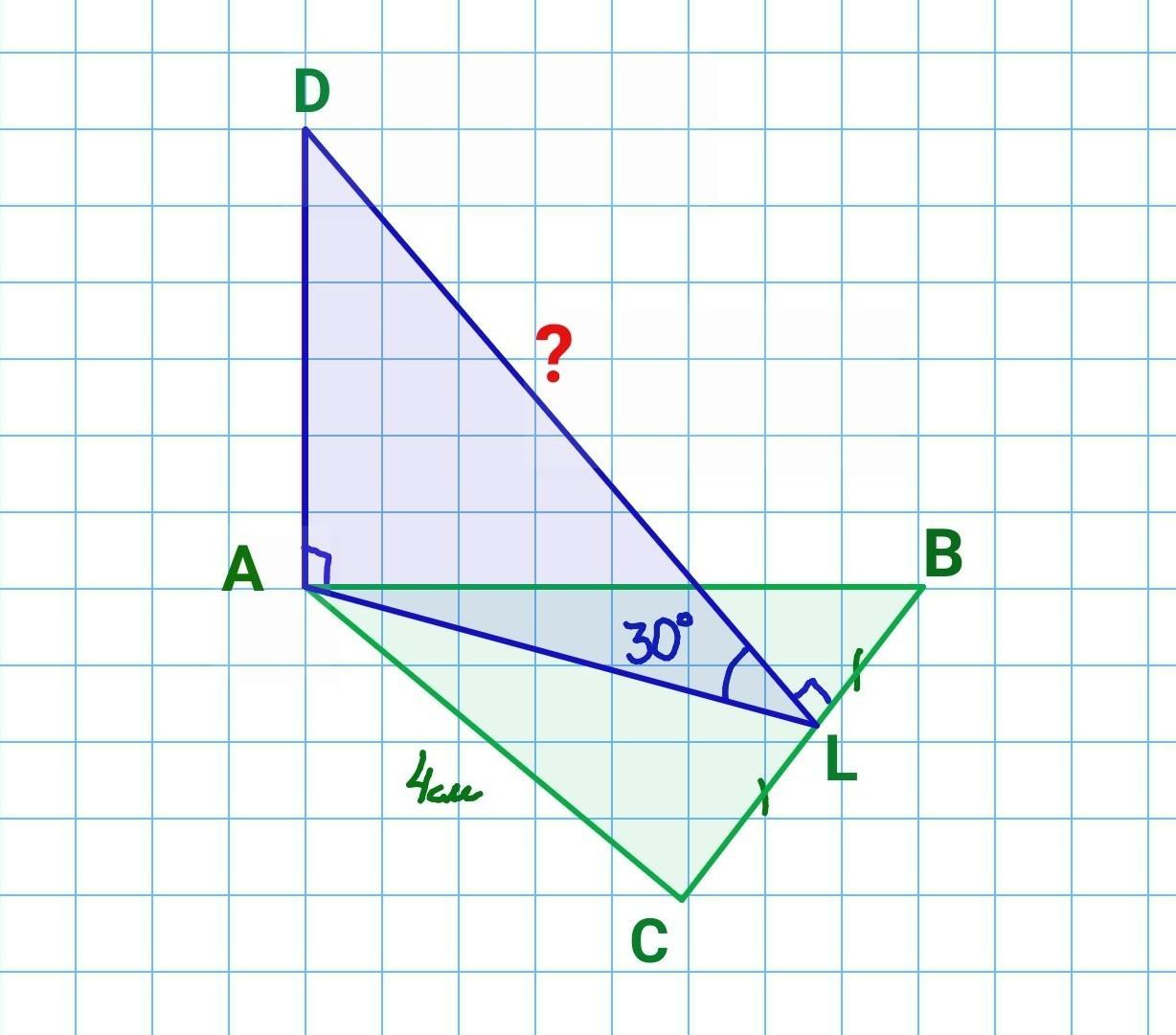
До площини рівностороннього трикутника ABC проведено перпендикуляр DA. Точка L - середина сторони BC. Кут між прямою DL і площиною трикутника дорівнює 30 градусів. Знайдіть відстань від точки D до прямої BC якщо AC дорівнює 4 см

Answer 1

Ответ:

Відстань від точки D до прямої ВС дорівнює 4 см

Объяснение:

До площини рівностороннього трикутника ABC проведено перпендикуляр DA. Точка L - середина сторони BC. Кут між прямою DL і площиною трикутника дорівнює 30 градусів. Знайдіть відстань від точки D до прямої BC якщо AC дорівнює 4 см.

Розв'язання

Маємо △АВС зі сторонами AB =BC=AC=4 см. За умовою DA⟂(ABC), тому (за властивістю) DA перпендикулярна до кожної прямої, що належить площині ABC.

Відстань від точки D до сторони BC трикутника - перпендикуляр опущений з точки D на пряму BC, тобто DL⟂BC.

Проведемо відрізок AL. Оскільки DA - перпендикуляр до площини ABC, то DL - похила (L - основа похилої), а відрізок AL - проекція похилої на площину ABC. Так як DL⟂BC, то за теоремою про три перпендикуляри (якщо відрізок, який проведений через основу похилої перпендикулярний до похилої, то він перпендикулярний і до ії проекції, і навпаки), тобто:

AL⟂BC.

Тому:

• ∠ALD - кут між DL і площиною трикутника АВС. ∠ALD=30°.
• AL - висота △ABC, а висота рівнобедреного трикутника є его медіаною: BL=CL=BC:2=4:2=2(см).

Розглянемо прямокутний трикутник ALC(∠L=90°).

Гіпотенуза AC=4см, катет CL=2см.

За теоремою Піфагора знайдемо катет AL.

AL²=AC²-CL²=4²-2²=16-4=12

AL=2√3(см)

Розглянемо прямокутний трикутник DAL(∠A=90°).

• Косинус гострого кута прямокутного трикутника - це відношення прилеглого катета до гіпотенузи.

$\bf cos \angle ALD = \dfrac{AL}{DL}$

$cos 30^\circ = \dfrac{2 \sqrt{3} }{DL}$

$\dfrac{ \sqrt{3} }{2} = \dfrac{2 \sqrt{3} }{DL}$

$DL = \dfrac{2 \times 2 \sqrt{3} }{ \sqrt{3} } = 4$ (см)

Відповідь: DL=4 см

#SPJ1