Question

КРУГИ ЭЙЛЕРА!

58 человек ежедневно добираются на работу общественным транспортом: на автобусе, или на метро. Каждый пользуется хотя бы одним из видов транспорта. 42 человека из них используют метро, 32- трамвай, 44 автобус. 21 человек из них используют метро и трамвай, 31 метро и автобус, 22-трамвай и автобус. Сколько среди них человек, которые используют все три вида транспорта, чтобы добраться на работу? ​

Answer 1

Обозначим:

$A$ - множество людей, использующих автобус

$M$ - множество людей, использующих метро

$T$ - множество людей, использующих трамвай

$A\cap M$ - множество людей, использующих автобус и метро

$A\cap T$ - множество людей, использующих автобус и трамвай

$M\cap T$ - множество людей, использующих метро и трамвай

$A\cup M\cup T$ - множество людей, использующих или автобус или метро или трамвай

Нас интересует следующее множество:

$A\cap M\cap T$ - множество людей, использующих и автобус и метро и трамвай

По условию:

$|A|=44;\ |M|=42;\ |T|=32;$

$|A\cap M|=31;\ |A\cap T|=22;\ |M\cap T|=11;$

$|A\cup M\cup T|=58$

Формула включений-исключений:

$|A\cup M\cup T|=|A|+|M|+|T|-|A\cap M|-|A\cap T|-|M\cap T|+|A\cap M\cap T|$

Отсюда:

$|A\cap M\cap T|=|A\cup M\cup T|-|A|-|M|-|T|+|A\cap M|+|A\cap T|+|M\cap T|$

Получим:

$|A\cap M\cap T|=58-44-42-32+31+22+21=14$

Ответ: 14 человек используют все три вида транспорта

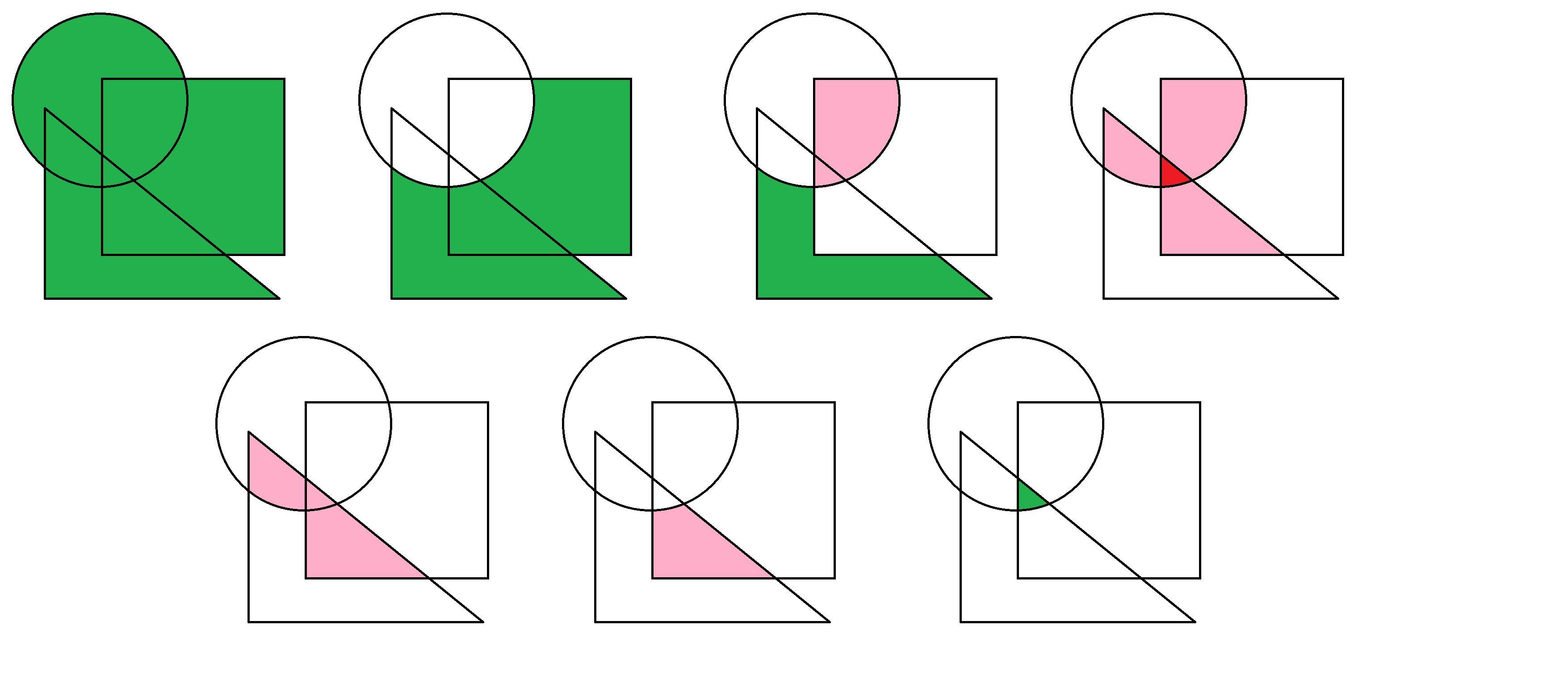
Примерный подсчет с использованием кругов Эйлера показан на картинке.

Зеленый цвет - часть учтена 1 раз

Белый цвет - часть не учтена

Розовый цвет - часть отнята 1 раз

Красный цвет - часть отнята 2 раза

Описание картинок:

1) Взято объединение трех множеств.

2) Отняли первое множество (круг).

3) Отняли второе множество (квадрат).

4) Отняли третье множество (треугольник).

Видно, что некоторые части (пересечения двух множеств) мы отняли лишний раз, а одну часть (пересечение трех множеств) мы лишний раз отняли дважды. Эти части нужно каким-то образом вернуть.

5) Добавили пересечение первого и второго множества (круга и квадрата).

6) Добавили пересечение первого и третьего множества (круга и треугольника).

7) Добавили пересечение второго и третьего множества (квадрата и треугольника).

В результата получено только пересечение трех множеств, которое нам и требуется.

Таким образом, действительно, от мощности объединения трех множеств нужно вычесть мощность каждого множества, а затем добавить мощность каждого попарного пересечения.