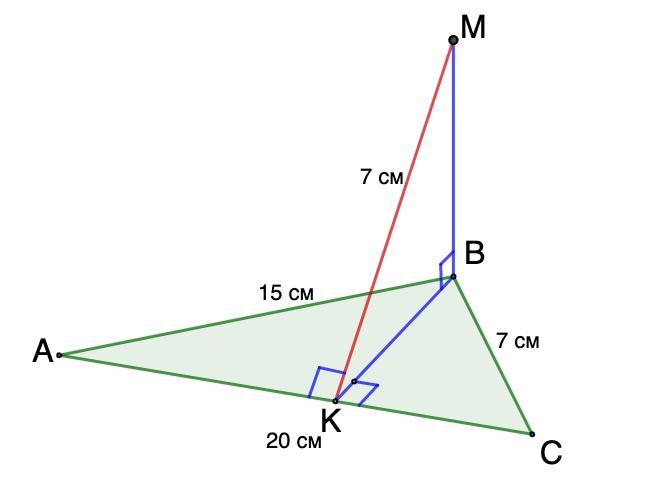
Сторони трикутника дорівнюють 7 см. 15 см і 20 см. З вершини найбільшого кута трикутника до його площини проведено перпендикуляр, i з другого його кінця до протилежної цьому куту сторони проведено перпендикуляр завдовжки 7 см. Знайдіть довжину перпендикуляра. проведеного до площини трикутника.
Ответы
Ответ:
Длина перпендикуляра к плоскости треугольника равна 5,6 см.
Объяснение:
Стороны треугольника равны 7 см, 15 см и 20 см. Из вершины наибольшего угла треугольника к его плоскости проведен перпендикуляр, и с второго его конца к противоположной этому углу стороны проведен перпендикуляр длиной 7 см. Найдите длину перпендикуляра к плоскости треугольника.
Дано: ΔАВС;
ВС = 7 см, АВ = 15 см, АС = 20 см.
МВ ⊥ АВС; МК ⊥ АС.
МК = 7 см.
Найти: МВ.
Решение:
- Против большей стороны в треугольнике лежит больший угол.
1. Соединим точку К с точкой В.
- Прямая, проведённая в плоскости через основание наклонной, перпендикулярная к самой наклонной, перпендикулярна её проекции на эту плоскость.
⇒ КВ ⊥ АС
2. Рассмотрим ΔАВС.
По формуле Герона найдем его площадь.
,
где р - полупериметр, a,b,c - стороны треугольника.
ВС = 7 см, АВ = 15 см, АС = 20 см.
р = (7 + 15 + 20) : 2 = 21 (см)
С другой стороны:
- Площадь треугольника равна половине произведения стороны на высоту, проведенную к этой стороне.
3. Рассмотрим ΔКМВ - прямоугольный.
По теореме Пифагора найдем МВ:
МВ² = КМ² - ВК² = 49 - 17,64 = 31,36 ⇒ МВ = √31,36 = 5,6 (см)
Длина перпендикуляра к плоскости треугольника равна 5,6 см.
#SPJ1