Предмет: Алгебра,
автор: Hilazhdxhxj
помогите пж пж п жпьжп
дам 100 БАЛЛОВ
Приложения:
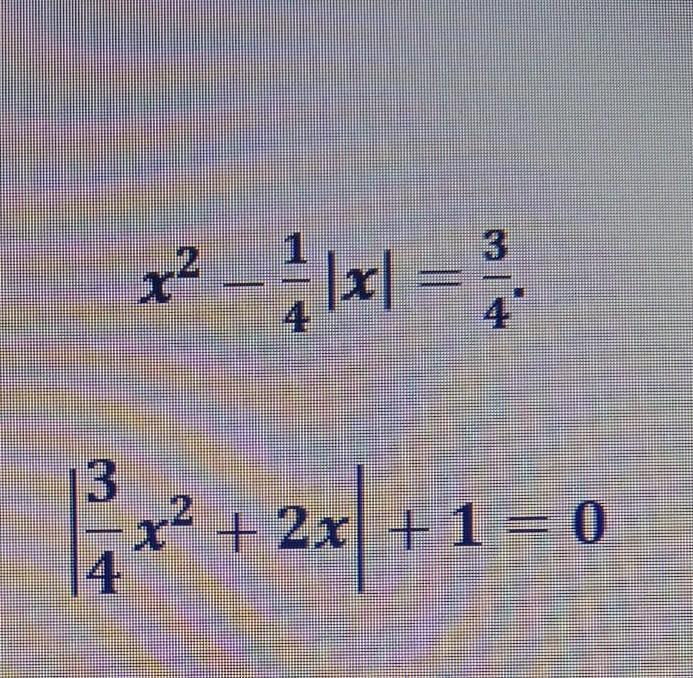
Simba2017:
второе решений не имеет
Ответы
Автор ответа:
1
Ответ:
Свойство модуля: . Поэтому можно уравнение переписать так
Замена:
Ответ:
Рассмотрим два случая.
причём
Значения переменной не входят в указанный промежуток, поэтому нет решений .
причём
Ответ: нет решений .
спасибо огромное !!!
Похожие вопросы
Предмет: Немецкий язык,
автор: polinamarkovskaja
Предмет: Математика,
автор: gerda1208
Предмет: Математика,
автор: dashkalashmilash
Предмет: Русский язык,
автор: panaabc00