Question

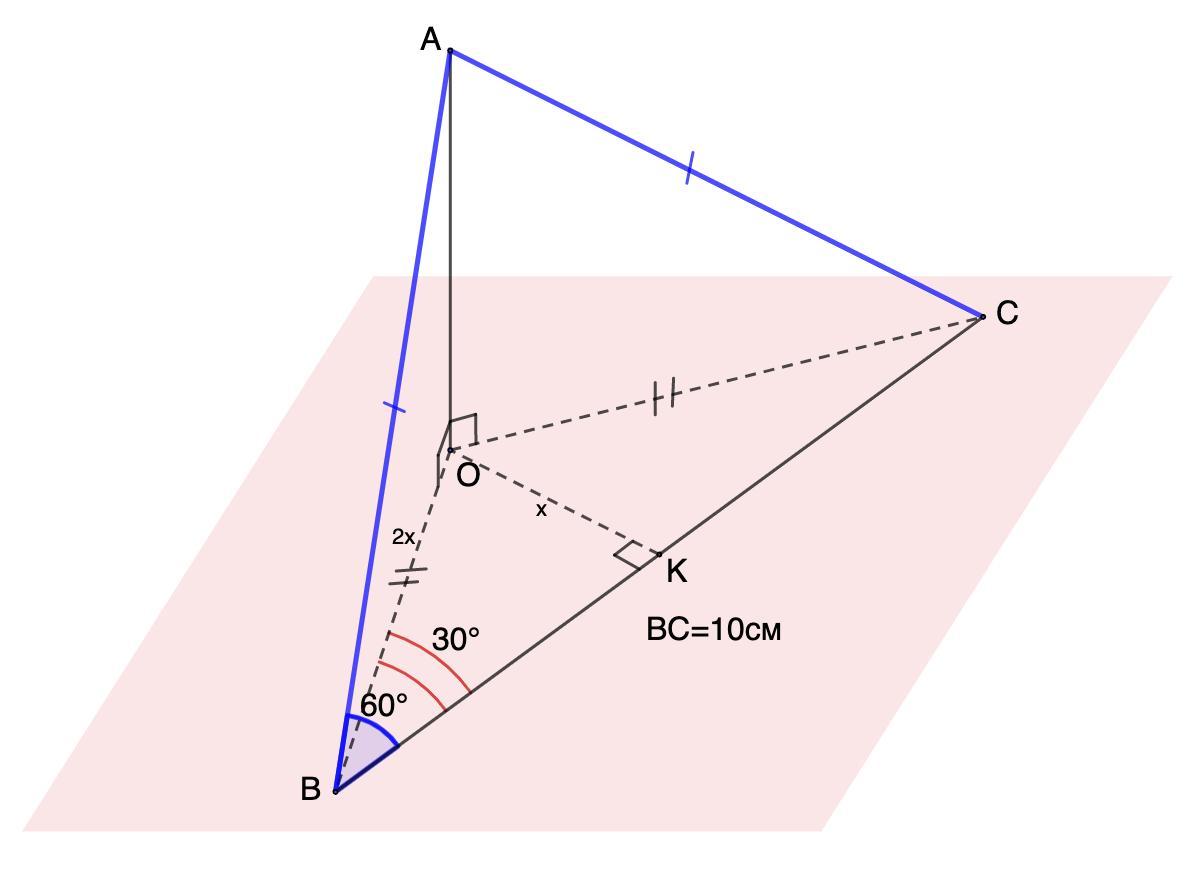
Із точки А,взятої поза площиною альфа,проведено до неї рівні похилі АВ і АС. Відстань ВС між основами похилих дорівнює 10 см. Кут між ВС і АВ дорівнює 60°,кут між ВС і проекцією похилої АВ на площину альфа -30°. Знайти відстань від точки А до площини альфа.​

Answer 1

Ответ:

Расстояние от точки А до плоскости α равно $\displaystyle \frac{10\sqrt{6} }{3}$  см.

Объяснение:

Из точки А, взятой вне плоскости α, проведены к ней равные наклонные АВ и АС. Расстояние ВС между основаниями наклонных равно 10 см. Угол между ВС и АВ равен 60°, угол между ВС и проекцией наклонной АВ на плоскость α - 30°. Найти расстояние от точки А до плоскости α.​

Дано: α;  А ∉ α;

АВ = АС - наклонные;

ВС = 10 см;

ВО - проекция АВ на α;

∠АВС = 60°; ∠ОВС = 30°.

Найти: АО.

Решение:

Проведем ОК ⊥ ВС.

1. Рассмотрим ΔВАС - равнобедренный (АВ = АС)

∠АВС = 60°

• Углы при основании равнобедренного треугольника равны.

⇒ ∠АВС = ∠АСВ = 60°

• Сумма углов треугольника равна 180°.

⇒ ∠ВАС = 180° - (60° + 60°) = 60°

ΔВАС - равносторонний.

⇒ ВА = АС = ВС = 10 см

2. Рассмотрим ΔВОС.

• Если равны наклонный, то и равны их проекции.

⇒ ΔВОС - равнобедренный.

• В равнобедренном треугольнике высота, проведенная к основанию, является медианой.

⇒ ВК = КС = 5 см.

3. Рассмотрим ΔВОК - прямоугольный.

Пусть ОК = х см.

• Катет, лежащий против угла в 30°, равен половине гипотенузы.

⇒ ОВ = 2х см

По теореме Пифагора:

ОВ² = ОК² + КВ²

4х² = х² + 25

3х² = 25   ⇒ х² = 25/3

ОВ² = 4х² = 100/3

4. Рассмотрим ΔВАО - прямоугольный.

По теореме Пифагора найдем АО:

АО² = ВА² - ОВ² = 100 - 100/3 = 200/3

$\displaystyle AO = \sqrt{\frac{200}{3} } =\frac{10\sqrt{2} }{\sqrt{3} }=\frac{10\sqrt{6} }{3} \;\;\;_{(CM)}$

Расстояние от точки А до плоскости α равно $\displaystyle \frac{10\sqrt{6} }{3}$  см.

#SPJ1