Question

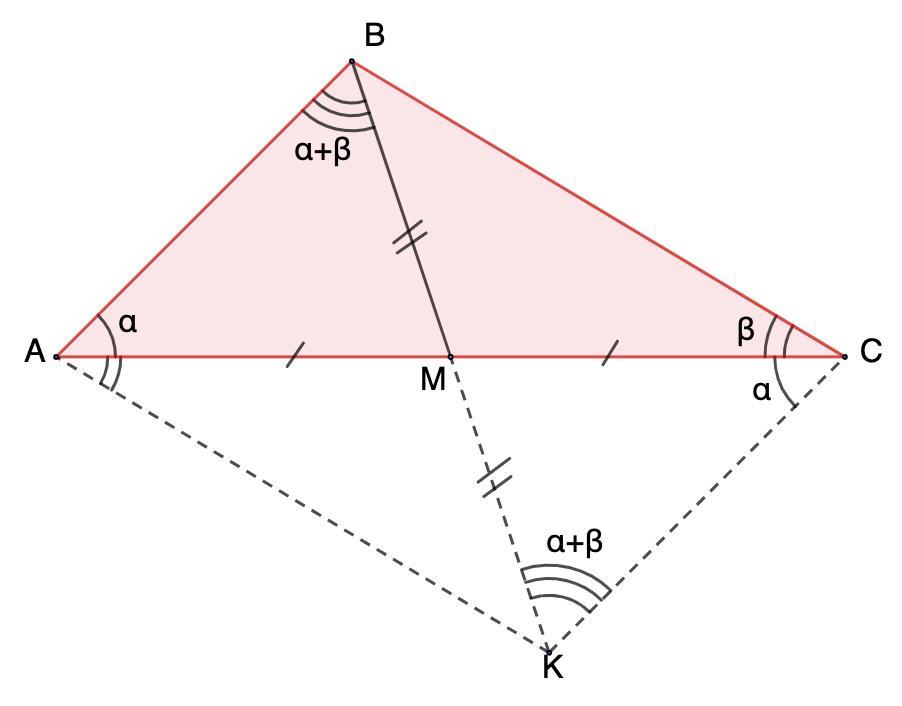
В треугольнике АВС провели медиану ВМ. Оказалось, что сумма углов А и С равна углу АВМ. Найдите отношение длин отрезков ВМ и ВС.
!!!Нужна картинка и с обьяснением!!!

Answer 1

Ответ:

Отношение длин отрезков ВМ и ВС равно 1 : 2.

Объяснение:

В треугольнике АВС провели медиану ВМ. Оказалось, что сумма углов А и С равна углу АВМ. Найдите отношение длин отрезков ВМ и ВС.

Дано: ΔАВС;

ВМ - медиана;

∠ВАС + ∠ВСА = ∠АВМ

Найти: ВМ : ВС

Решение:

Задача на удвоение медианы.

Продлим ВМ на отрезок МК = ВМ. Соединим точку К с А и С.

Получили четырехугольник АВСК.

Обозначим ∠ВАС = α; ∠ВСА = β ⇒ ∠АВМ = α+β

1. Рассмотрим АВСК.

АС и ВК - диагонали.

АМ = МС (ВМ - медиана);

ВМ = МК (построение)

• Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник - параллелограмм.

⇒ АВСК - параллелограмм.

2. Рассмотрим ΔКВС.

∠ВАС = ∠АСК = α (накрест лежащие при АВ || КС и секущей АС)

∠АВК = ∠ВКС = α+β (накрест лежащие при АВ || КС и секущей ВК)

∠ВСК = ∠АСК + ∠ВСА = α+β

⇒ ∠ВСК = ∠ВКС = α+β  

• Если в треугольнике равны два угла, то этот треугольник равнобедренный.

⇒ КВ = ВС

ВМ = 1/2 ВК

⇒ ВС : ВС = 1 : 2

Отношение длин отрезков ВМ и ВС равно 1 : 2.

#SPJ1