Question

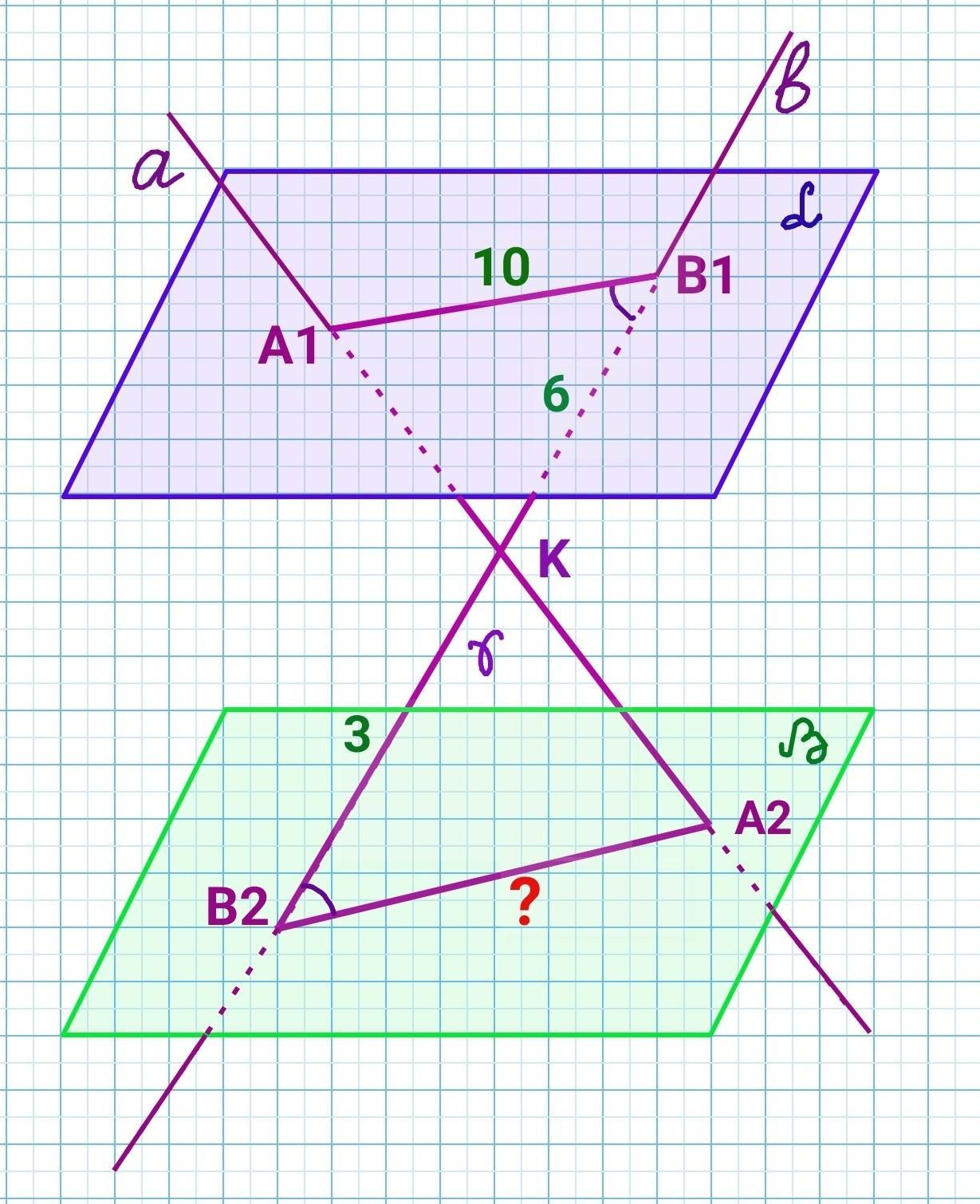
Площини α і β паралельні. Через точку К, що лежить між цими площинами проведено прямі a і b, які перетинають площину α в точках А1 і В1, а площину β в точках А2 і В2 відповідно. Знайдіть довжину відрізка А2 В2, якщо А1В1 = 10 см, КВ1= 6 см, КВ2=3см

З рисунком

Answer 1

Ответ:

Довжина відрізка А2В2 дорівнює 5 см

Объяснение:

Площини α і β паралельні. Через точку К, що лежить між цими площинами проведено прямі a і b, які перетинають площину α в точках А1 і В1, а площину β в точках А2 і В2 відповідно. Знайдіть довжину відрізка А2В2, якщо А1В1 = 10 см, КВ1= 6 см, КВ2=3см

• Через дві прямі, що перетинаються, можна провести площину, і до того ж тільки ОДНУ. (наслідок з аксіом стереометрії).
• Якщо дві паралельні площини перетинаються третьою, то прямі перетину паралельні (властивість)
• Якщо два кутиодного трикутника відповідно дорівнюють двом кутам другого, то такі трикутники подібні (ознака).
• У подібних трикутників відповідні сторони пропорційні (властивість).

Розв'язання

1) Через прямі а і b, що перетинаються, проведемо площину Ɣ. Ця площина перетинає площину α по прямій А1В1, а площину β по прямій А2В2.

2) За властивістю паралельних площин маємо:

А1В1 || А2В2

3)∠А1В1В2=∠В1В2А2 - як внутрішні різносторонні кути при перетині паралельних прямих А1В1 і А2В2 січною В1В2

4)∠А1КВ1=∠А2КВ2 - як вертикальні

5) Тому △А1В1К і △А2В2К подібні за двома кутами.

6) Отже:

$\sf \dfrac{A_1B_1}{A_2B_2} = \dfrac{B_1K}{B2K}$

$\sf \dfrac{10}{A_2B_2} = \dfrac{6}{3}$

$\sf A_2B_2 = \dfrac{10\cdot3}{6} = \dfrac{30}{6} = \bf 5$ см

Відповідь: 5 см

#SPJ1