1.Исследовать свойства и построить график функции (вместо А подставить 1)
2. Найти площадь фигуры ограниченной линиями (вместо В подставить 1)
помогите пожалуйста решить
40 баллов

Ответы
Ответ:
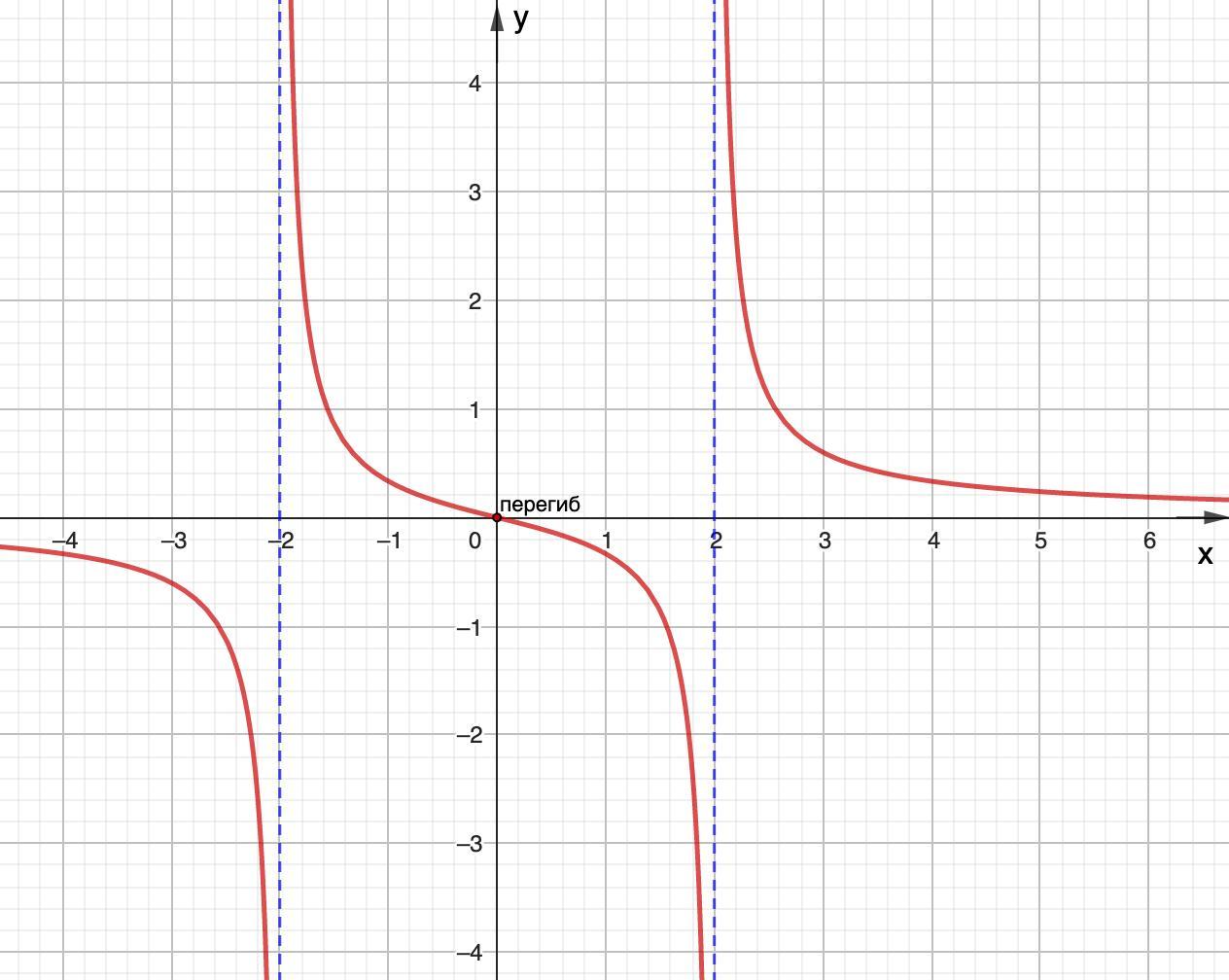
1.
1)
2) функция нечетная.
3) График пересекает ось Ох в точке (0; 0)
4) x = ± 2 - вертикальные асимптоты. y = 0 - горизонтальная асимптота.
5) функция убывает на промежутках: (-∞;-2); (-2;2); (2;+∞)
6) функция выпукла на промежутках: (-∞; -2); [0; 2),
функция вогнута на промежутках: (-2; 0]; (2; +∞)
2.
площадь фигуры, ограниченной линиями:
равна ед.²
Объяснение:
1. Исследовать свойства и построить график:
2. Найти площадь фигуры, ограниченной линиями:
1.
1) Область определения функции:
2) Четность, нечетность.
y(-x) = - y(x) ⇒ функция нечетная.
3) Нули функции.
График пересекает ось Ох в точке (0; 0)
4) Асимптоты.
Вертикальная:
⇒ x = ± 2 - вертикальные асимптоты.
Наклонная у = kx + b
⇒ y = 0 - горизонтальная асимптота.
5) Возрастание, убывание.
Найдем производную, приравняем к нулю и найдем корни. Отметим их на числовой оси и определим знаки производной на промежутках.
y' отрицательна при любых значениях х, в точках х = ±2 производная не существует.
- Если "+" - функция возрастает, если "-" - функция убывает.
⇒ функция убывает на промежутках: (-∞;-2); (-2;2); (2;+∞)
6) Выпуклость вогнутость.
Найдем производную второго порядка:
Приравняем вторую производную к нулю и найдем корни.
х = 0; х ≠ ±2
Знаки на промежутках:
- Если производная второго порядка положительна, функция вогнута, если отрицательна - выпукла.
⇒ функция выпукла на промежутках: (-∞; -2); [0; 2),
функция вогнута на промежутках: (-2; 0]; (2; +∞)
Строим график.
2.
- Площадь фигуры найдем по формуле:
Слева функция ограничена прямой х = -1, справа х = 2, снизу у = 0.
Найдем точку пересечения первых двух функций:
Данное равенство верно только при х = 0
Изобразим данные графики. Искомая площадь состоит из двух площадей:
S = S₁ + S₂
Найдем S₁.
Здесь f₂(x) = eˣ; f₁(x) = 0; b = 0; a = -1
Найдем S₂:
Здесь f₂(x) = 1/(x+1); f₁(x) = 0; b = 2; a = 0
#SPJ1