Предмет: Алгебра,
автор: danilshebanov15
Завдання за 83 балів!
Приложения:

Ответы
Автор ответа:
1
Объяснение:
Відповідь на фото. Вибачайте за почерк
Приложения:
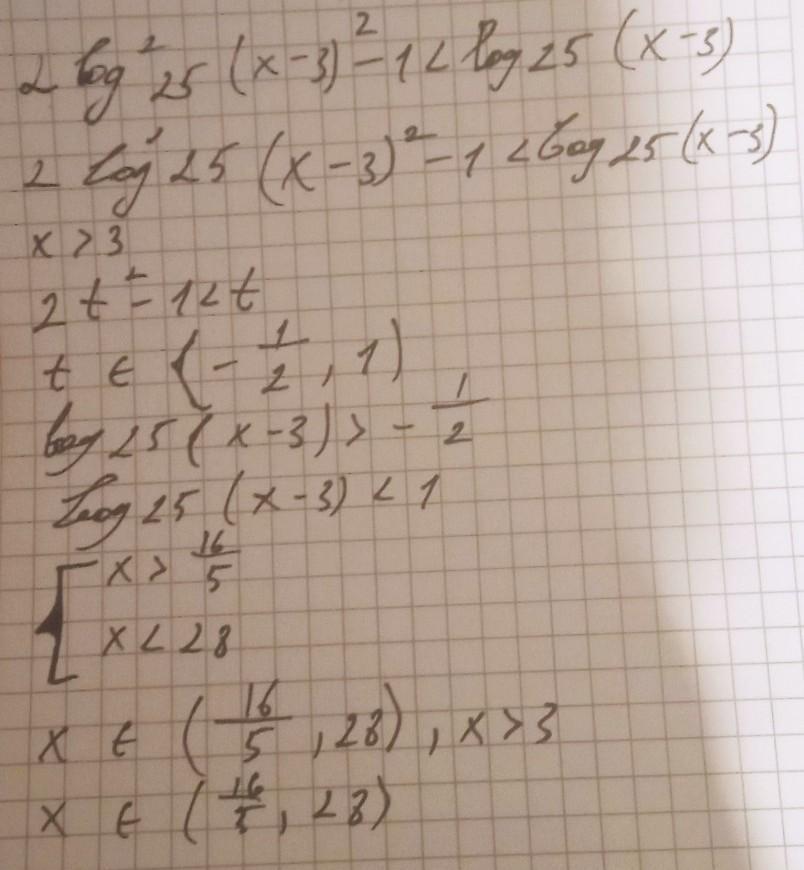
danilshebanov15:
Бездогано!(Почерк схожий на мій)Велике дякую!
Автор ответа:
1
Спасибо большое
РазжевалА :)
Похожие вопросы
Предмет: Алгебра,
автор: daniela1847j
Предмет: Математика,
автор: mari8353
Предмет: Литература,
автор: arisha2kon
Предмет: Математика,
автор: KoteikaSK
Предмет: Русский язык,
автор: kirilllololoshcka