Question

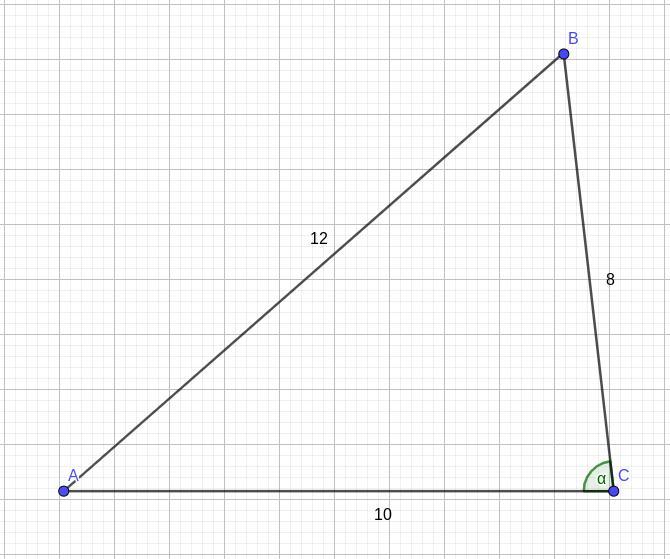
Стороны треугольника 12 см, 10 см и 8 см. Найдите косинус угла треугольника, лежащего против большей стороны.​

Answer 1

Ответ:

$\cos \ \alpha = 0.125$

Объяснение:

Из теоремы косинусов выводим формулу косинуса угла:

$a^{2} = b^{2} + c^{2} - 2 * b* c * \cos \ \alpha$

$\displaystyle\cos \ \alpha = \frac{b^{2}+c^{2}-a^{2}}{2*b*c}$

Заменяем переменные на данные из задачи и находим ответ:

$\displaystyle\cos \ \alpha = \frac{BC^{2}+AC^{2}-AB^{2}}{2*8*10}$

$\displaystyle\cos \ \alpha = \frac{8^{2}+10^{2}-12^{2}}{160} = \frac{164-144}{160} = \frac{20}{160}= 0.125$