Вариант 2 1. Если периметр квадрата равен 48 см, то площадь квадра- та равна: a) 12 см2; б) 48 см2; в) 144 см2; г) 120 см2. 2. Дан прямоугольник площадью 42 см², одна из его сторон равна 7 см. Найдите периметр прямоугольника. 3. BK - высота параллелограмма, опущенная на сторону AD (рис. 1), ZD=135°, BK = 6 см, KD = 8 см. Найдите площадь параллелограмма. B A K Puc. 1 4. Дан треугольник АВС (рис. 2). ВК= 8 см и АМ = 6 см высо- ты треугольника, АС = 15 см. - Найдите длину стороны ВС. D A В K M Puc. 2 C 5. Периметр ромба равен 40 см, произведение диагоналей равно 192 см². Найдите высоту ромба. Помогите срочно пжжж) даю 20 баллов
Ответы
Ответ:
1. Площадь квадрата равна квадрату его стороны. Периметр квадрата равен сумме длин всех его сторон. Так как у квадрата четыре стороны и они все равны, тогда P=4*a, где а - сторона квадрата.
Так как периметр равен 48 см, вычислим сторону квадрата.
48=4*а;
а=48/4;
а=12 cм.
Зная, что сторона равна 12 см, вычислим площадь.
S=a^2=12^2=12*12=144 cм^2.
ответ В) 144см^2
2. Площадь прямоугольника находим по формуле S = a · b,
где S - площадь прямоугольника, a и b - его стороны.
Периметр прямоугольника находим по формуле Р = 2 · (а + b),
где P - периметр прямоугольника, a и b - его стороны.
По условию: площадь S = 42 см²,
одна сторона равна а = 7 см,
тогда вторая сторона равна: b = 42 : 7 = 6 (см).
Следовательно периметр будет равен Р = 2 · (7 + 6) = 2 · 13 = 26 (см).
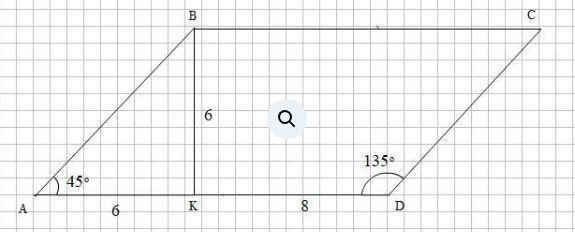
3. Смотри рисунок в прикрепленном файле.
∠А + ∠D = 180° как углы, прилежащие к одной из сторон (к стороне AD) параллелограмма, отсюда ∠А = 180° - ∠D = 180° - 135° = 45°.
Прямоугольный треугольник АВК является равнобедренным, так как ∠А = 45° и ∠АВК = 90° - 45° = 45°, поэтому АК = ВК = 6см.
Сторона AD = АК + KD = 6 + 8 = 14(см)
Площадь параллелограмма S = AD · BK = 14 · 6 = 84(cм²)
4. Площадь треугольника: S=1/2ha , где h - высота и а - сторона, к которой она проведена.
S=1/2*BK*AC
S=15*8/2=60 cм².
S=1/2*AM*BC
BC=2S/AM
BC=2*60/6=20 см
5. Периметр ромба равен Р=4*L, где L - длина стороны,
следовательно L = Р/4 = 40/4 = 10 см.
Произведение диагоналей ромба = 2*S, где S - площадь Ромба, то есть S = 192/2 = 96 см². С другой стороны, S = L*h, где h - искомая высота. Отсюда находим h = S/L = 96/10 = 9.6 см.
Пошаговое объяснение: