Предмет: Алгебра,
автор: ciellllll
Помогите пожалуйста... только нужно прям расписать задание•́ ‿ ,•̀
Приложения:
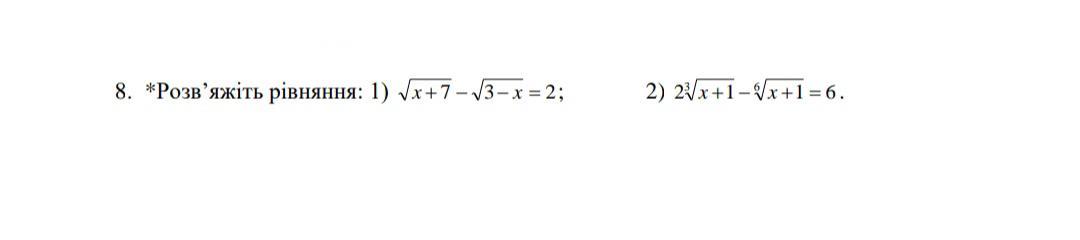
ThisIsNotAChristmas:
У-у-у-у, дай мне время. Тут о-о-очень длинное решение будет..
Хорошо, спасибо!
Ответы
Автор ответа:
0
Объяснение:
P.S ≠ означает что решений нет. (я просто не знал как ещё это изобразить.)
И вот как это можно понимать...в любом случае спасибо за твое старание!
Это удивление, или упрёк?"
Конечно же удивление, восхищаюсь умными людьми
Похожие вопросы
Предмет: Математика,
автор: rafiq9
Предмет: Математика,
автор: yuliimg500
Предмет: Қазақ тiлi,
автор: stas7289
Предмет: Химия,
автор: anastasiaraboslikk