Предмет: Математика,
автор: yaroslavprudivus12
поможіть 30 балів фастом пжжж
Приложения:
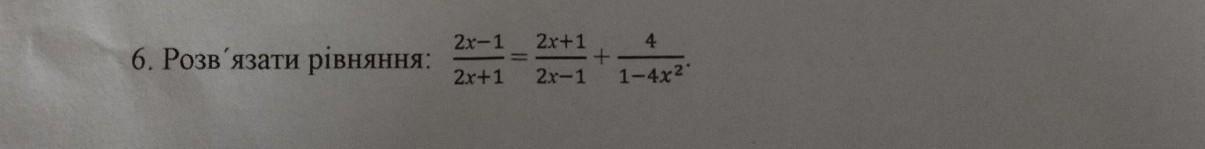
Ответы
Автор ответа:
1
Ответ:
Уравнение не имеет решения, то есть x∈∅
Пошаговое объяснение:
Перевод: Решите уравнение:
Решение. Определим множество допустимых значений уравнения:
Так как x=0,5 не принадлежит множеству допустимых значений уравнения, то уравнение не имеет решения.
#SPJ1
Похожие вопросы
Предмет: Українська мова,
автор: reznikvlad0
Предмет: Литература,
автор: nadiavisocina09
Предмет: Математика,
автор: oaiskdjdjjuedi
Предмет: Химия,
автор: kravec4
Предмет: Литература,
автор: idiliya84