Предмет: Алгебра,
автор: nazarjurchak76
ПОМОГИТЕ СРОЧНО ПОЖАЛУЙСТА
Приложения:
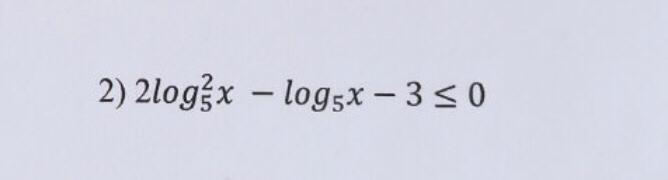
Ответы
Автор ответа:
1
Ответ:
Ответ: х ∈ [1/5; 5√5]
Объяснение:
Решить неравенство:
- Число логарифма положительно.
ОДЗ: х > 0
Выполним замену переменной:
Получим неравенство и решим его методом интервалов:
Обратная замена:
Так как основание логарифма 5 > 1, то
Ответ: х ∈ [1/5; 5√5]
Похожие вопросы
Предмет: Алгебра,
автор: boldyrevdenis19
Предмет: Українська література,
автор: martunyk202201
Предмет: История,
автор: sonyakonst22
Предмет: Математика,
автор: mzazerskij
Предмет: Математика,
автор: ivanovaAA2007