Предмет: Алгебра,
автор: letvik878
Помогите решить эти уравнения дам 50 балов
Приложения:
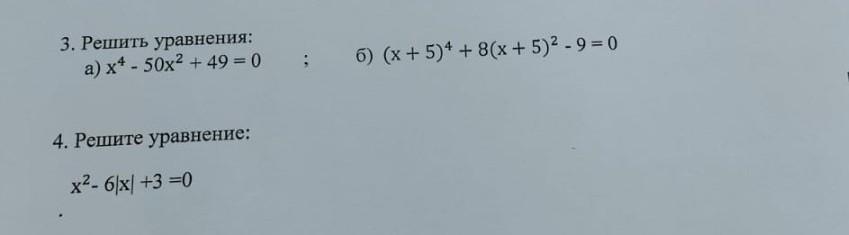
Ответы
Автор ответа:
2
Ответ:
3а) Биквадратное уравнение . Решаем с помощью замены переменной .
3б) Биквадратное уравнение . Тоже решаем с помощью замены переменной.
4) Воспользуемся свойством модуля: и решим с помощью замены переменной .
letvik878:
спасибо вам ют
Похожие вопросы
Предмет: Английский язык,
автор: brynzamarina8
Предмет: Биология,
автор: d9455054
Предмет: География,
автор: lizamarkina175
Предмет: Геометрия,
автор: REDEMAX34
Предмет: Математика,
автор: anaracalova39678