Question

При якому значенні коефіцієнта а графік функції у = ах2 + (а – 4)х – 4,5 має з віссю абсцис одну спільну точку?

Якщо таких значень декілька, то у відповідь запишіть їх добуток.

Answer 1

Ответ:

При а = -2 и а = -8  данный график имеет с осью абсцисс одну общую точку.

Произведение коэффициентов равно 16.

Объяснение:

При каком значении коэффициента а график функции

у = ах² + (а – 4)х – 4,5

имеет с осью абсцисс одну общую точку?

Если таких значений несколько, то в ответ запишите их произведение.

Если график пересекает ось Ох, то у = 0.

ах² + (а – 4)х – 4,5 = 0

Если D = 0, то уравнение имеет один корень.

D = (a - 4)² - 4 · a · (-4,5) = a² - 8a + 16 + 18a = a² + 10a + 16

Получили квадратное уравнение. Решим его.

a² + 10a + 16 = 0

D = 100 - 4 · 16 = 36   ⇒   √D = 6

$\displaystyle a_1=\frac{-10+6}{2}=-2;\;\;\;\;\;a_2=\frac{-10-6}{2} =-8$

⇒ При а = -2 и а = -8  данный график имеет с осью абсцисс одну общую точку.

Тогда данная функция имеет вид:

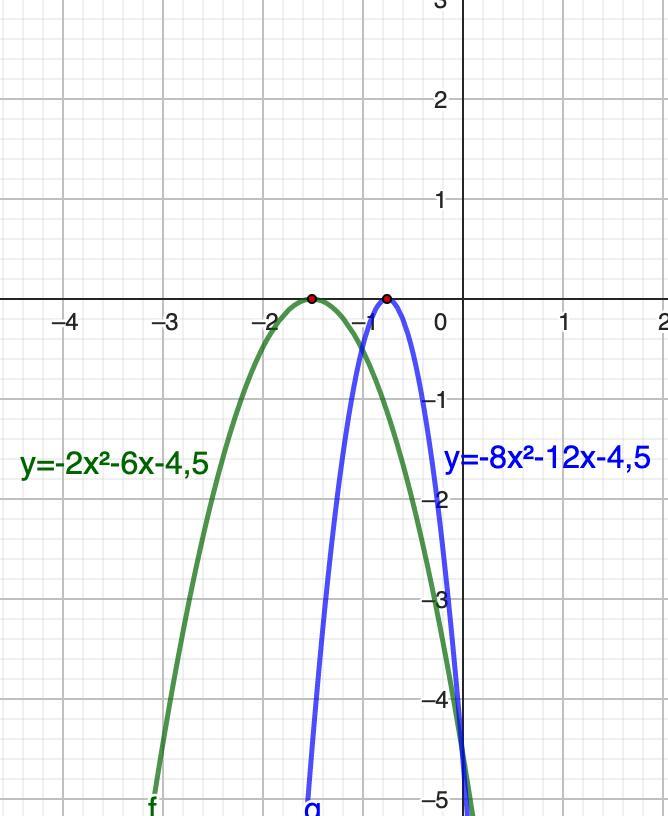
у = -2х² - 6х - 4,5   и   у = -8х² - 12х - 4,5

Произведение коэффициентов равно:

-2 · (-8) = 16

#SPJ1

Answer 2

Ответ:

16

Объяснение:

Перевод: При каком значении коэффициента а график функции у=а·x²+(а–4)·х–4,5 имеет с осью абсцисс одну общую точку?

Если таких значений несколько, то в ответ запишите их произведение.

Нужно знать: График параболы у=а·x²+b·х+c касается (то есть имеет одну общую точку) с осью абсцисс, если D=b²–4·a·c=0. При этом точка касания будет вершиной параболы.

Решение. Проверим условие D=0:

(a-4)²–4·a·(–4,5)=0

a²–8·a+16+18·a=0

a²+10·a+16=0

a²+2·a+8·a+16=0

a·(a+2)+8·(a+2)=0

(a+8)·(a+2)=0

a+8=0 или a+2=0

a = –8 или a = –2.

По условию находим произведение: (–8)·(–2) = 16.

#SPJ1