Question

Терміново!!!!!!!


2). Обчисліть суму всіх значень функції у=х 3/2 , якщо 1<х≤25

а. 144
б 224
с. 304
д. 0
е. 624



​

Answer 1

Ответ:

2) Ответ: б. 224

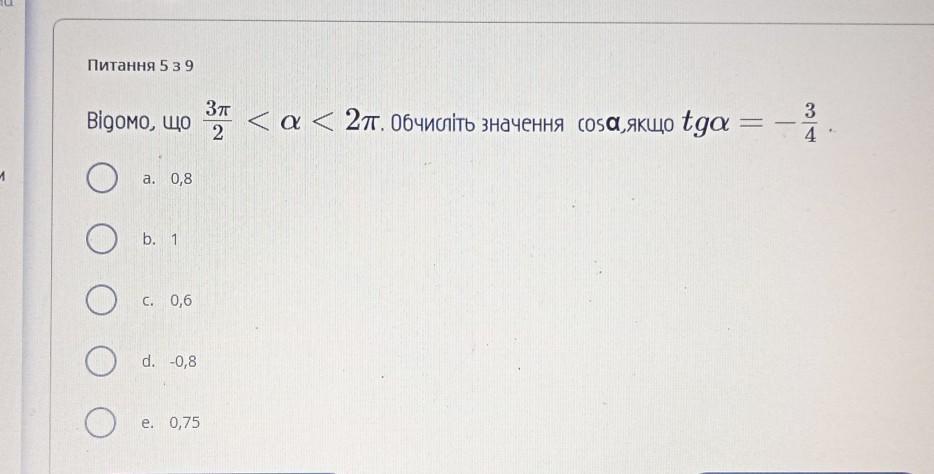
5) Ответ: а. 0,8

Объяснение:

Уточненное задание:

2). Вычислите сумму всех целых значений функции $\displaystyle y=x^{\frac{3}{2} }$ , если 1 < х ≤ 25.

5) Известно, что $\displaystyle \frac{3\pi }{2} < \alpha < 2\pi$. Вычислите значение cosα, если tgα = $\displaystyle -\frac{3}{4}$.

2)  $\displaystyle y=x^{\frac{3}{2} }$

Преобразуем данное выражение:

$\displaystyle x^{\frac{3}{2} }=\sqrt{x^3} =\sqrt{x^2\cdot x} =x\sqrt{x}$

Дан интервал 1 < х ≤ 25.

Числа,  из которых корень извлекается целым числом:

4, 9, 16, 25.

Вычислим значения функции:

y(4) = 4 · √4 = 4 · 2 = 8

y(9) = 9 · √9 = 9 · 3 = 27

y(16) = 16 · √16 = 16 · 4 = 64

y(25) = 25 · √25 = 25 · 5 = 125

Найдем сумму этих чисел:

8 + 27 + 64 + 125 = 224

Ответ: б. 224

5) Найти $cos\;\alpha$,  если   $\displaystyle tg\;\alpha = -\frac{3}{4};\;\;\;\frac{3\pi }{2} < \alpha < 2\pi$.

В IV четверти тангенс отрицательный, косинус положительный.

Воспользуемся формулой:

$\boxed {\displaystyle\bf tg^2\;\alpha +1=\frac{1}{cos^2\;\alpha } }$

$\displaystyle \frac{9}{16}+1=\frac{1}{cos^2\;\alpha }\\ \\ \frac{25}{16}=\frac{1}{cos^2\;\alpha } \\\\cos^2\;\alpha =\frac{16}{25} \\\\cos\;\alpha =\pm\frac{4}{5}$

Так как  в IV четверти cos α > 0, то ответ:

$\displaystyle cos\;\alpha =\frac{4}{5}=0,8$

Ответ: а. 0,8

#SPJ1