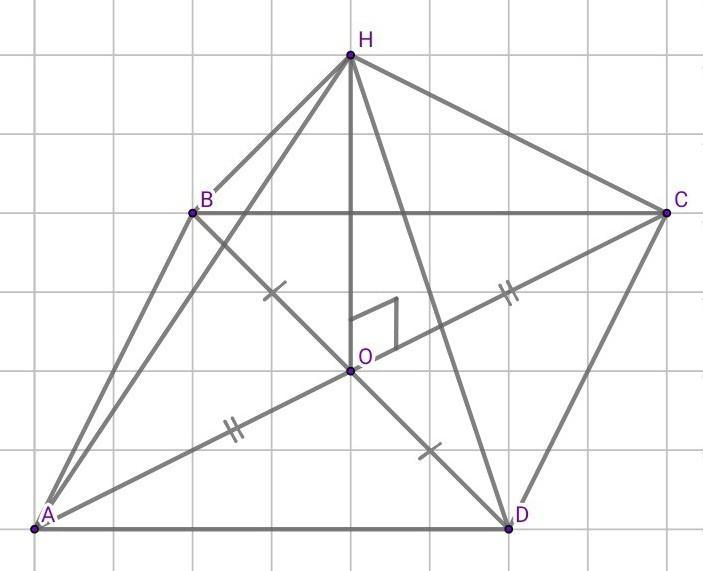
Через точку О пересечения диагоналей параллелограмма ABCD проведена прямая ОН, перпендикулярная к плоскости параллелограмма. Докажите, что HA= HC, HB= HD.
Ответы
Ответ:
см.объяснение
Пошаговое объяснение:
1)Докажите , что HA = HC
Доказательство:
Рассм. прямоугольные ∆-ки АOН и COH , НА и НС - наклонные к (АВС) , АО и СО - проекции наклонных НА и НС на (АВС) соответственно , так как диагонали параллелограмма точкой пересечения делятся пополам , то проекции АО = СО . Согласно свойству наклонных выходящих из одной точки : Если проекции равны , то равны и их наклонные ⇒ НА = НС , что и требовалось доказать
2)Докажите , что НВ = НD
Доказательство:
Рассм. прямоугольные ∆-ки ВОН и DOH , НВ и НD - наклонные к (АВС) , ВО и DO - проекции наклонных НВ и НD на (АВС) соответственно , так как диагонали параллелограмма точкой пересечения делятся пополам , то проекции ВО = DO . Согласно свойству наклонных выходящих из одной точки : Если проекции равны , то равны и их наклонные ⇒ HB = HD , что и требовалось доказать