Предмет: Геометрия,
автор: aleksandrasolomka1
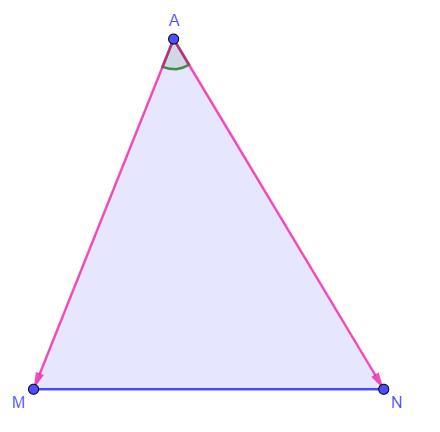
Трикутник MAN – рівнобедрений з основою MN, а його бічна сторона дорівнює 7. Знайдіть косинус кута між векторами (AM) ⃗ і (AN) ⃗, якщо (AM) ⃗∙(AN) ⃗=14
Ответы
Автор ответа:
10
Ответ:
Косинус угла между векторами:
Объяснение:
Дано: 7 см,
Найти:
Решение:
По определению скалярного произведение векторов:
#SPJ1
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: lesovakarina9
Предмет: Беларуская мова,
автор: mishanyabelsky
Предмет: Математика,
автор: daria4723
Предмет: Английский язык,
автор: Аноним
Предмет: Литература,
автор: roman76artel