Предмет: Алгебра,
автор: ImXoxolFromKharkiv
ПОХІДНА ФУНКЦІЇ 11 КЛАСС
Приложения:
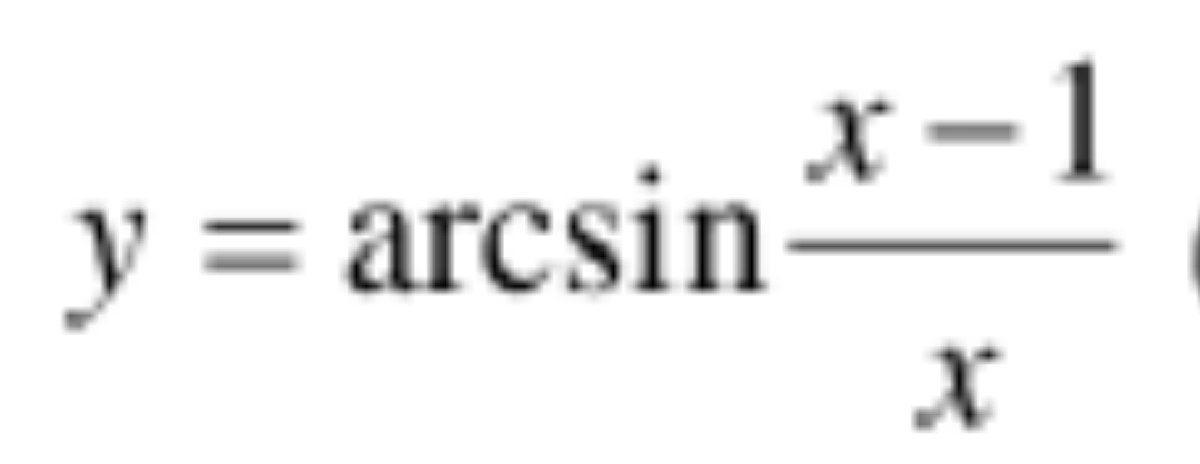
Ответы
Автор ответа:
1
Ответ:
Найдём производную:
Вычислим производную частного:
ImXoxolFromKharkiv:
Лучший, братик
Похожие вопросы
Предмет: Математика,
автор: warden123456787676
Предмет: Биология,
автор: polidasa552
Предмет: Математика,
автор: vladhristov042
Предмет: Математика,
автор: Sergeybykov2019