Question

Бічні ребра трикутної піраміди рівні, а плоскі кути при вершині піраміди - прямі. Площа основи піраміди 9$\sqrt{3}$ см2. Знайдіть площу бічної поверхні піраміди.

дам 60 баллов

Answer 1

Ответ:

Площадь боковой поверхности пирамиды равна 27 см².

Пошаговое объяснение:

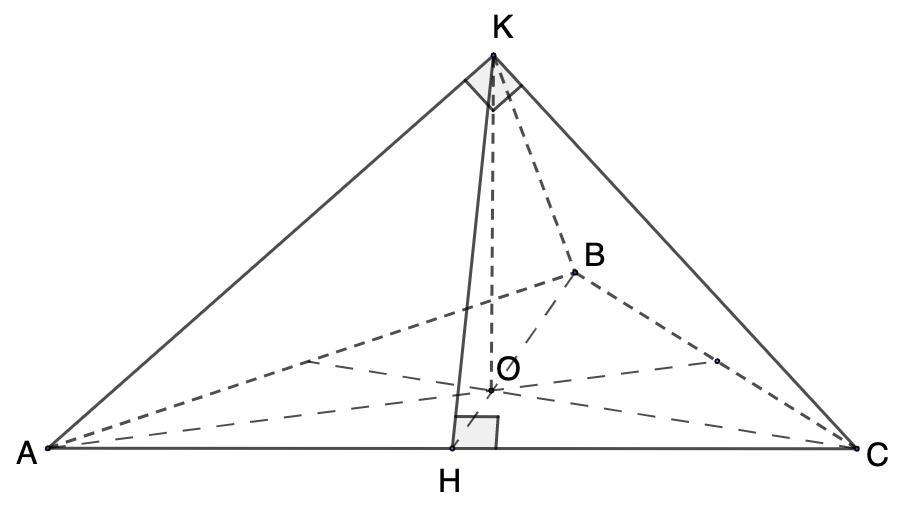
Боковые ребра треугольной пирамиды ровные, а плоские углы при вершине пирамиды - прямые. Площадь основания пирамиды 9√3 см². Найдите площадь боковой поверхности пирамиды.

Дано: КАВС - пирамида;

КА = КВ = КС;

Sосн. = 9√3 см²;

∠АКС = ∠ВКС = ∠АКВ = 90°

Найти: Sбок.

Решение:

• Формула площади боковой поверхности пирамиды:
• $\displaystyle \bf S_{bok.}=\frac{1}{2}PL$ , где Р - периметр основания, L - образующая.

Рассмотрим ΔКАВ, ΔВКС, ΔАКС - прямоугольные.

КА = КВ = КС (условие)

⇒ ΔКАВ = ΔВКС = ΔАКС (по двум катетам)

АВ = ВС = АС (как соответственные элементы)

                 

Рассмотрим ΔАВС.

АВ = ВС = АС   ⇒ ΔАВС - равносторонний.

• Формула площади равностороннего треугольника:
• $\displaystyle \bf S=\frac{a^2\sqrt{3} }{4}$ ,где а - сторона треугольника.

Подставим S = 9√3 см²

$\displaystyle \bf 9\sqrt{3} =\frac{a^2\sqrt{3} }{4}\\\\a^2=\frac{9\sqrt{3}\cdot4 }{\sqrt{3} } =36\\\\a=6$

⇒ АВ = ВС = АС = 6 см

Р(АВС) = 6 · 3 = 18 (см)

Найдем образующую КН.

Рассмотрим ΔАКС - прямоугольный, равнобедренный.

∠КАС = ∠КСА = 90° : 2 = 45° (углы при основании равнобедренного треугольника)

• В равнобедренном треугольнике высота, проведенная к основанию, является медианой и биссектрисой.

⇒ АН = НС = 6 : 2 = 3 (см)

∠АКН = ∠НКС = 90° : 2 = 45°

Рассмотрим ΔАКН - прямоугольный.

∠КАН = ∠АКН = 45° ⇒ ΔАКН - равнобедренный.

АН = НК = 3 см.

Можем найти площадь боковой поверхности:

$\displaystyle \bf S_{bok}=\frac{1}{2}\cdot 18\cdot 3 = 27$ (см²)

Площадь боковой поверхности пирамиды равна 27 см².

#SPJ1