Предмет: Математика,
автор: Dead2016j
Упростить выражение
![\sqrt[3]{\frac{3x}{y^2} } : \sqrt[3]{\frac{y}{9x^2} } \sqrt[3]{\frac{3x}{y^2} } : \sqrt[3]{\frac{y}{9x^2} }](https://tex.z-dn.net/?f=%5Csqrt%5B3%5D%7B%5Cfrac%7B3x%7D%7By%5E2%7D+%7D+%3A+%5Csqrt%5B3%5D%7B%5Cfrac%7By%7D%7B9x%5E2%7D+%7D)
Приложения:
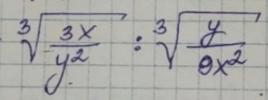
Ответы
Автор ответа:
1
Ответ:
Автор ответа:
1
Ответ:
3х/у
Пошаговое объяснение:
1)
Частное корней одной степени равно корню из частного подкоренных выражений
2) Чтобы разделить на дробь, необходимо сделать умножение на выражение, обратное этой дроби
3)Умножьте дроби
4)Вычислить кубический корень
5) ответ: 3х/у
Приложения:
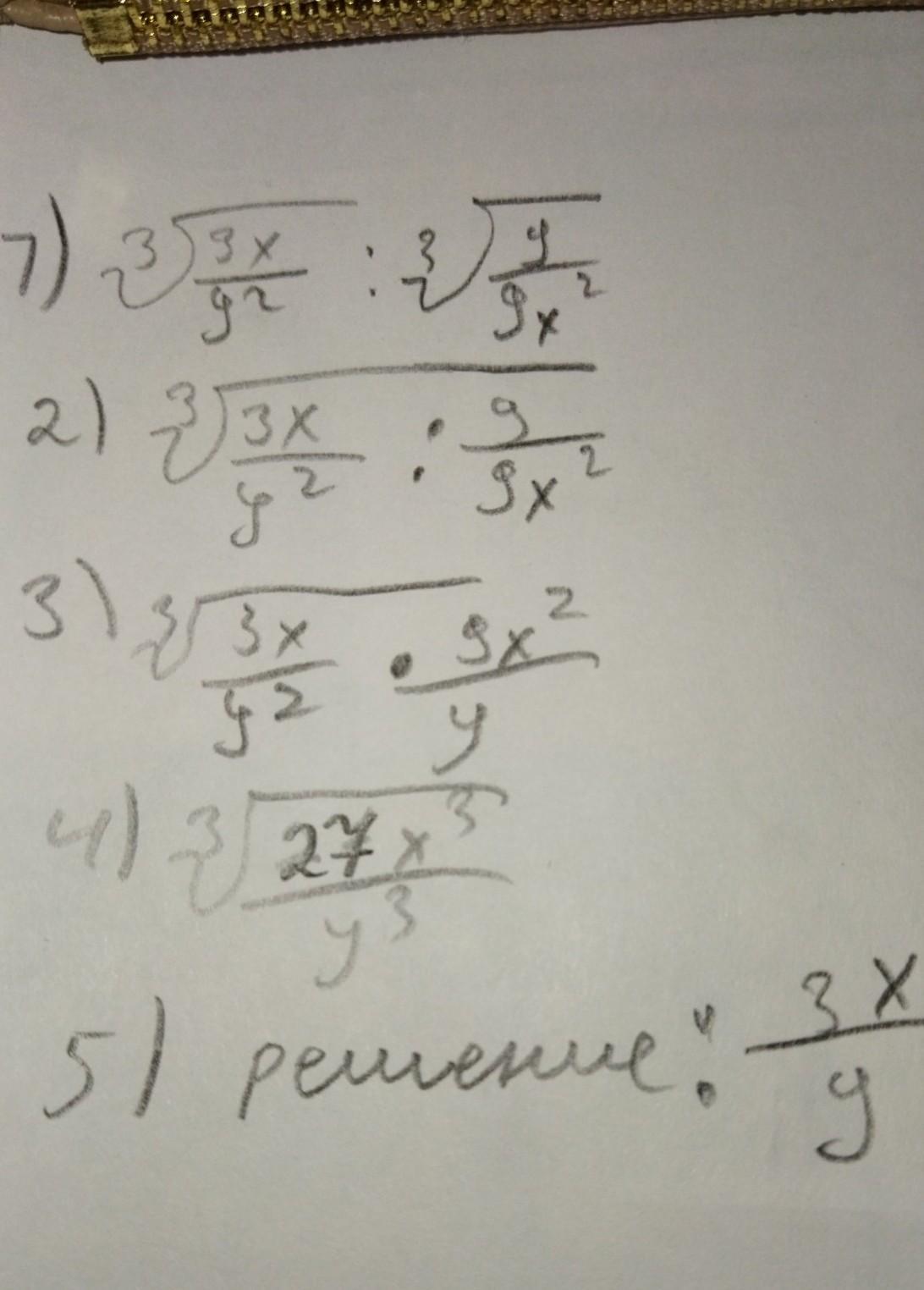
Похожие вопросы
Предмет: Английский язык,
автор: arsenagent000
Предмет: Алгебра,
автор: leraponosara
Предмет: Русский язык,
автор: aliyaabdumutalipova
Предмет: География,
автор: Evelina300606
Предмет: Математика,
автор: krutik000