ДОПОМОЖІТЬ!!!
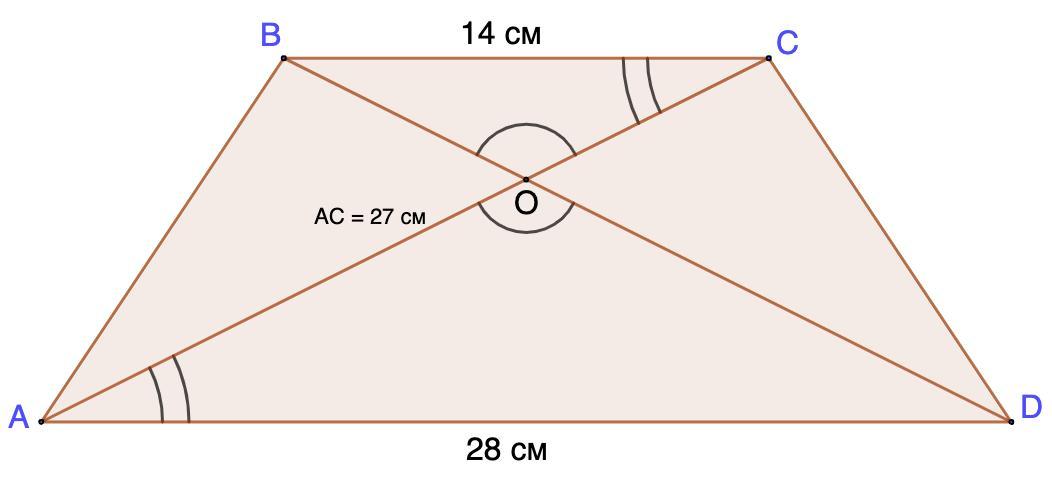
Основи рівнобічної трапеції дорівнюють 14 см та 28 см, а довжина її діагоналі становить 27 см. Знайдіть периметри трикутників ВСО і АDО, якщо О - точка перетину діагоналей трапеції.(з поясненням)
Даю 40 балів
Ответы
Ответ:
Периметры треугольников ВСО и АDО равны 32 см и 64 см соответственно.
Объяснение:
Основания равнобедренной трапеции равны 14 см и 28 см, а длина его диагонали составляет 27 см. Найдите периметры треугольников ВСО и АDО, если О - точка пересечения диагоналей трапеции.
Дано: АВСD - равнобедренная трапеция.
АС и BD - диагонали; АС ∩ BD = О;
ВС = 14 см; AD = 28 см; АС = 27 см.
Найти: Р(ВОС) и Р(АDО)
Решение:
Рассмотрим ΔВОС и ΔАDО.
- Вертикальные углы равны.
⇒ ∠ВОС = ∠АОD
- При пересечении двух параллельных прямых третьей накрест лежащие углы равны.
⇒ ∠ВСО = ∠ОАD (при ВС || AD и секущей АС)
ΔВОС ~ ΔАDО (по двум углам)
Запишем отношения сходственных сторон:
- Диагонали равнобедренной трапеции равны.
⇒ АС = BD = 27 см.
Пусть СО = х см, тогда ОА = 2х см
х + 2х = 27
х = 9
⇒ ОС = ОВ = 9 см.
- Периметр - сумма длин всех сторон.
Р(ВОС) = ОВ + ВС + ВО = 9 + 14 + 9 = 32 (см)
- Периметр подобных треугольников относятся как коэффициент подобия k.
Периметры треугольников ВСО и АDО равны 32 см и 64 см соответственно.
#SPJ1