Предмет: Геометрия,
автор: f22KEY
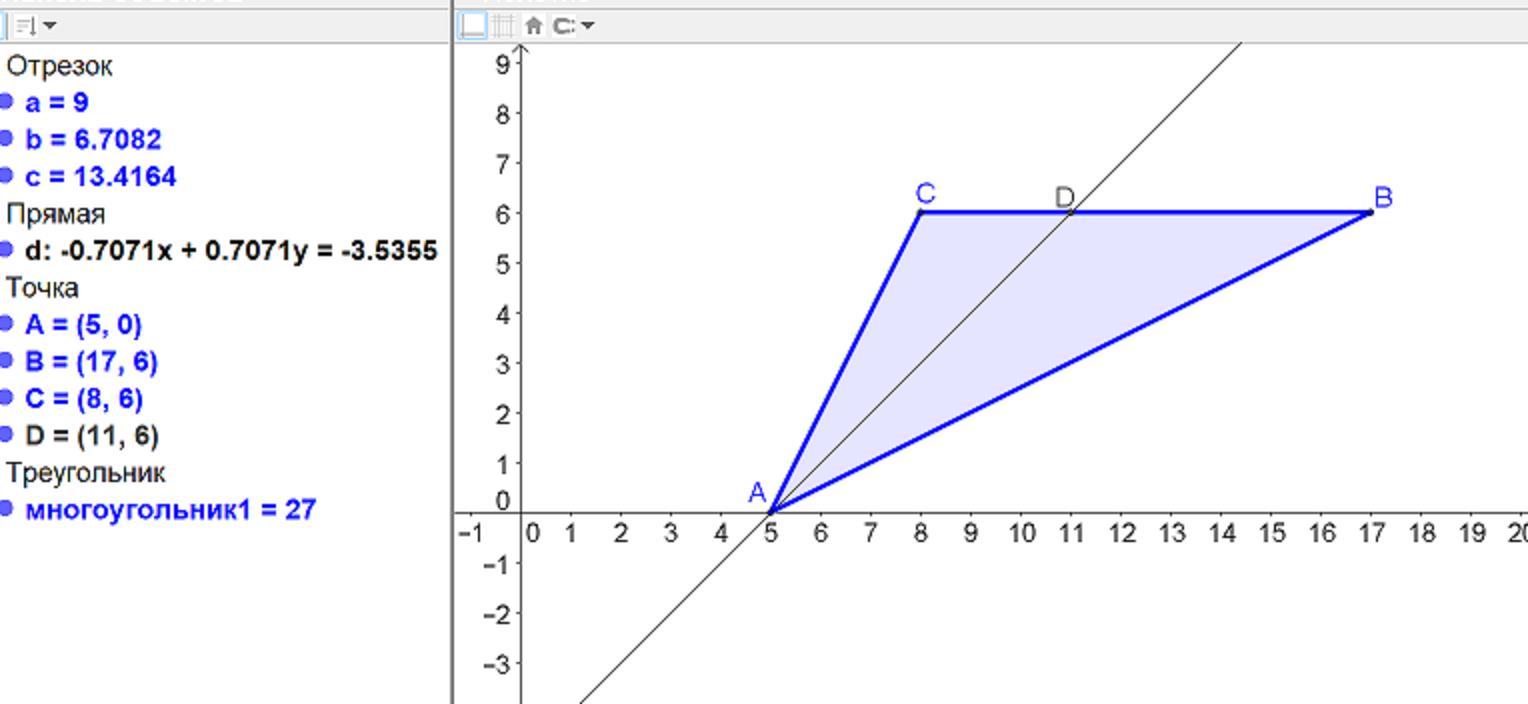
Вершины треугольника ABC имеют координаты A(5;0), B(17;6) и C(8;6). Биссектриса угла A пересекает сторону BC в точке D.
Найди координаты точки D.
Ответ: D(
;
).
Ответы
Автор ответа:
1
Находим уравнения прямых АВ и АС.
Вектор АВ = (17 – 5; 6 – 0) = (12; 6), k = 6/12 = 1/2.
Вектор АС = (8 – 5; 6 – 0) = (3; 6), k = 3/6 = 2.
Уравнение АВ: (х – 5)/12 = у/6 или х – 2у – 5 = 0 в общем виде.
Уравнение АС: (х – 5)/3 = у/6 или 2х – у – 10 = 0 в общем виде.
(х – 2у – 5)/√(1² + (-2)²) = +-(2х – у – 10)/√(2² + (-1)²).
Знаменатели равны, приравниваем числители.
1) х – 2у – 5 = +-(2х – у – 10),
х – 2у – 5 = 2х – у – 10,
х + у - 5 = 0, y = -x + 5.
2) х – 2у – 5 = -2х + у + 10,
3х – 3у – 15 = 0,
х - у - 5 = 0, y = x – 5 это и есть уравнение биссектрисы угла, так как угловой коэффициент при х положителен, как и у векторов АВ и АС.
Приложения:
Похожие вопросы
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: husdhreewrh
Предмет: Английский язык,
автор: jijiji0
Предмет: Химия,
автор: vikusentsiya17
Предмет: Биология,
автор: danahasanova957