Предмет: Алгебра,
автор: simeikoalena
Доведіть за допомогою векторів, що чотирикутник з вершинами в точках А(1; 5), B(7; 7), C(13; 5) 1 D(7; 3) - ромб.
Ответы
Автор ответа:
1
Объяснение:
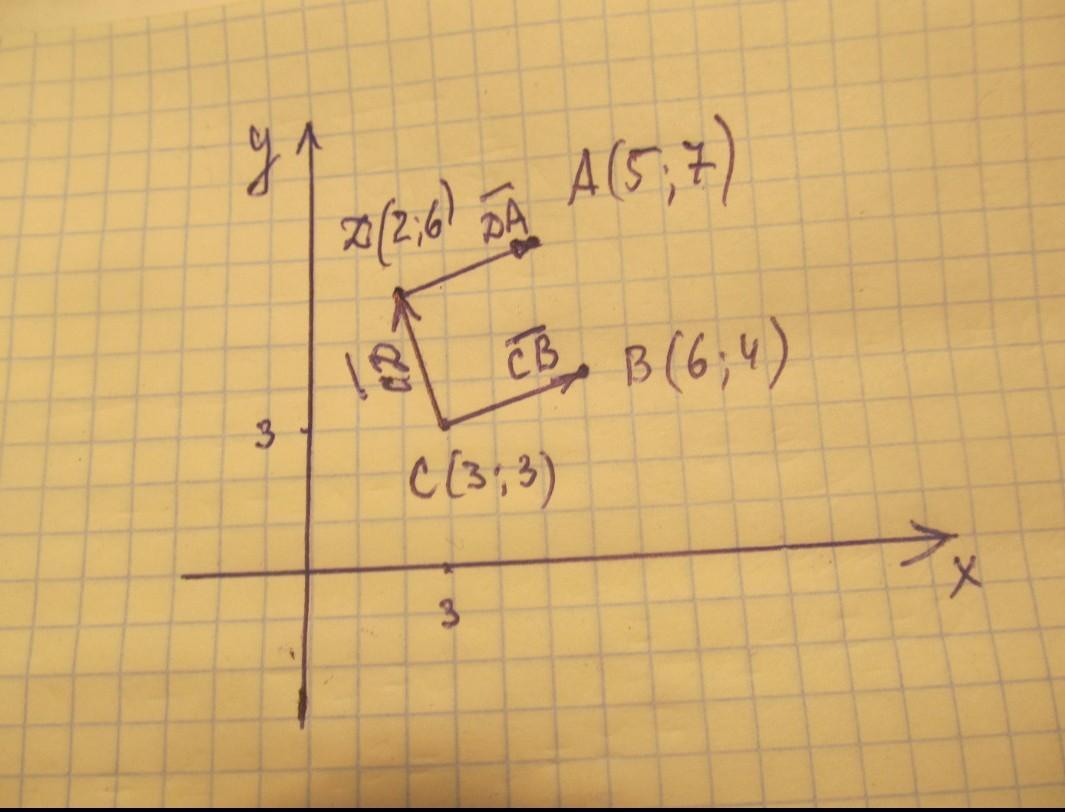
Координаты вектора=(х2-х1); (у2-y1)
ДА((5-2);(7-6))=(3;1)
векторы ДА и CB параллельны и равны; т.к. векторы имеют одинаковые координаты.
CB((6-3): (4-3)-(3:1)
АВСД - параллелограмм по признаку - противоположные стороны параллельны и равны.
ДА/=√(32+12)=√10; координаты вектора СД((2-3);
(6-3))=(-1;3)
IСДІ=v((-1)2+32)=√10
Смежные стороны параллелограмма равны.
Параллелограмм с равными сторонами - ромб.
Диагонали IСAI и IВДI равны по √20=2√5, значит АВСД не просто ромб, а квадрат))
Приложения:
Похожие вопросы