Question

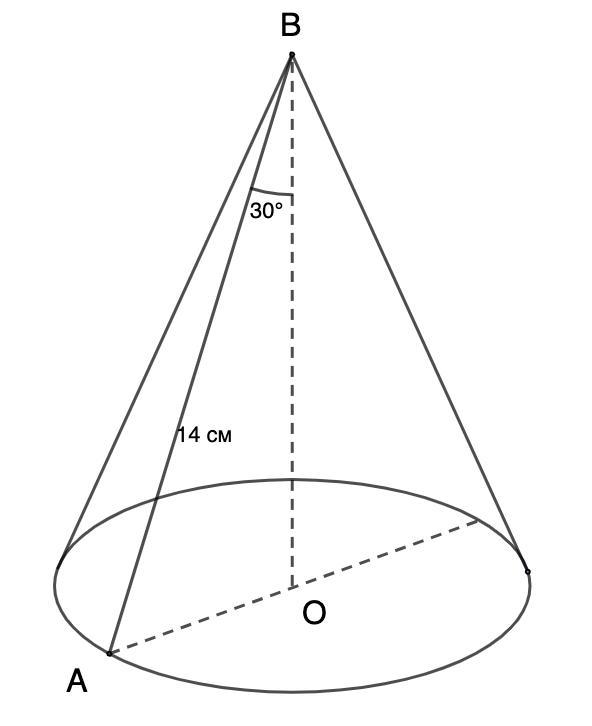
Кут між висотою і твірною конуса дорівнює 30 градусів. Знайдіть повну поверхню конуса, якщо твірна дорівнює 14см.

Answer 1

Ответ:

Площадь полной поверхности конуса равна 147π см².

Объяснение:

Угол между высотой и образующей конуса равен 30 градусам. Найдите полную поверхность конуса, если образующая равна 14 см.

Дано: конус;

∠АВО = 30°; ВА = 14 см - образующая.

Найти: S полной поверхности конуса.

Решение:

Площадь полной поверхности конуса найдем по формуле:

$\boxed { S = \pi R(R+l)}$ , где  R - радиус основания, l - образующая.

Образующая равна:

l = BA = 14 см.

Надо найти радиус основания конуса.

Рассмотрим ΔАВО - прямоугольный.

∠АВО = 30°

• Катет, лежащий против угла в 30°, равен половине гипотенузы.

⇒ АО = ВА : 2 = 14 : 2 = 7 (см)

Радиус равен 7 см.

Можем найти площадь полной поверхности конуса:

$S = \pi \cdot 7\cdot (7+14)=147\pi \;_{(CM^2)}$

Площадь полной поверхности конуса равна 147π см².

#SPJ1