Предмет: Геометрия,
автор: vertijanastasia90215
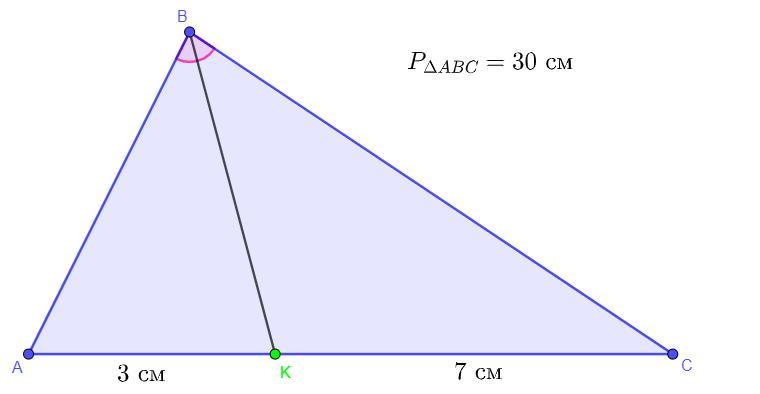
периметр трикутника дорівнює 30 см а його бісектриса ділить протилежну сторону на відрізки завдовжки 7см і 3 см .Знайдіть сторони трикутника.
Ответы
Автор ответа:
2
Відповідь:
Сторони трикутника дорівнють:
AC = 10 см
AB = 6 см
BC = 14 см
Пояснення:
Дано: 30 см, AK = 3 см, KC = 7 см, BK - бісектриса
Знайти: AB,BC,AC - ?
Розв'язання:
За основною властивістю відрізка:
AC = AK + KC = 3 см + 7 см = 10 см
За означенням периметра і теоремою про бісектрису складемо систему рівнянь:
см
см.
#SPJ1
Приложения:
Похожие вопросы
Предмет: Қазақ тiлi,
автор: muhamedzanovnaaziza
Предмет: Қазақ тiлi,
автор: s64757863
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: Bookfair
Предмет: Українська мова,
автор: prosto1girl