Question

Правильний восьмикутник вписаний у коло. Площа кругового сектора, що відповідає центральному куту восьмикутника, дорівнює 3π. Знайдіть площу восьмикутника. варіанти відповідей А) 6√2 ; Б) 48√2 ; В) 12√2; Г) 24√2. ​

Answer 1

Ответ: Площа восьмикутника дорівнює  Б) 48√2 (oд)²

Объяснение:

Центральный угол правильного n-го угольника можно найти по формуле :

$\alpha =\dfrac{360^\circ}{n}$

Таким образом :

$\alpha =\dfrac{360}{8} = 45^\circ$

Площадь кругового сектора можно найти с помощью формулы :

$S =\dfrac{\pi r^2}{360}\cdot \alpha$

где α - угол  заключенный между радиусами данного сектора .

Из условия задачи:

Площадь кругового сектора равна :  3π

т.е

$S =\dfrac{\pi r^2}{360}\cdot 45^{\circ} =3\pi \\\\\\\dfrac{\pi r^2}{8}= 3\pi \\\\ r^2 = 24$

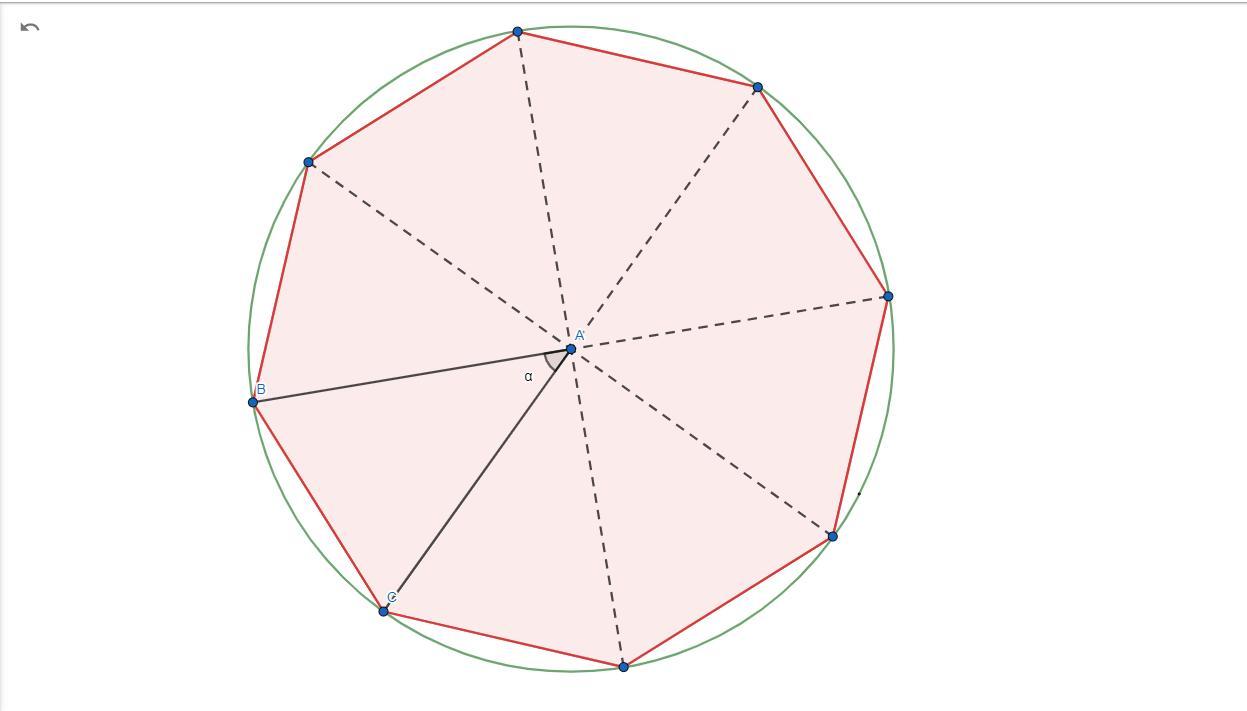
Проведя пунктирные линии из центра окружности к вершинам нашего восьмиугольника , мы можем заметить наш восьмиугольник можно разбить на 8 равных по площади треугольника , таким образом нам достаточно будет найти площадь  ΔABC ,  а затем умножить его площадь на 8.

С помощью формулы

$S_{\triangle}= \dfrac{1}{2}ab \cdot \sin \alpha$

Найдем площадь  ΔABC

В нашем случае  a = b = r = 8  ,  ∠α = 45°

$S_{\triangle}= \dfrac{1}{2} r \cdot r\cdot \sin 45^\circ = \dfrac{1}{2}\cdot r^2 \cdot \dfrac{\sqrt{2} }{2} =\dfrac{r^2\sqrt{2} }{4}$

Подставим  r² = 24

$S_{\triangle}= \dfrac{r^2\sqrt{2} }{4}=\dfrac{24\sqrt{2} }{4} = 6\sqrt{2}$

Теперь найдем  площадь  нашего восьмиугольника :

$S= 8S_{\triangle} = 8 \cdot 6\sqrt{2} = 48\sqrt{2}$

#SPJ1