Предмет: Алгебра,
автор: Sanya2263
Требуется помощь с определённым интегралом.
Приложения:
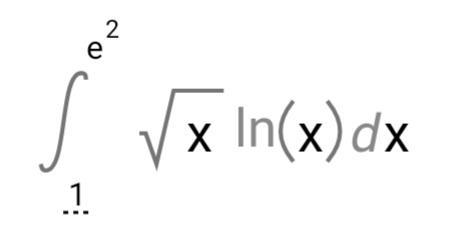
Ответы
Автор ответа:
1
Ответ:
1 слагаемое:u=ln(x)
2 слагаемое:dv=√x
дифференцируем первую часть:
интегрируем вторую часть:
пусть x=u², тогда:
дифференцируем обе части:
2u²du не в вверху...(\frac{}{} забыл просто)
пределы определённого интеграла:
himikomat:
ща скину
\frac{{u}^{3}}{3} снизу под 3 черта потом идёт предел и снизу предела(под чертой)u=√e² - (\frac{{u}^{3}}{3} снизу опять черта потом предел и снизу этой черты u=1)
\frac-это дробь
Насчёт фрак'а я понял
Вопрос по оформлению: писать ли прямо, что u=1 в знаменателе? И каков итоговый ответ?
u=1 после второго предела снизу
давайте я вам изображение скину как это выглядит на последний ваш вопрос, потом жб кинете если что чтоб ответ удалился, ок?
Всё, посмотрите последний свой вопрос
конечный ответ если упростить получится \frac{{8e}^{3}+4}{9}
*итоговый
Похожие вопросы
Предмет: Химия,
автор: kovalovartom9
Предмет: Математика,
автор: albinababko281
Предмет: Биология,
автор: Аноним
Предмет: Математика,
автор: Аноним
Предмет: Биология,
автор: oksankamedvedeva1989