Question

Допоможіть будь-ласка, благаю!!!!!!!!!!

Правильний восьмикутник вписаний у коло. Площа кругового сектора, що відповідає центральному куту восьмикутника, дорівнює 3π. Знайдіть площу восьмикутника. варіанти відповідей А) 6√2 ; Б) 48√2 ; В) 12√2; Г) 24√2.

(можна з розв'язанням , дуже прошу допоможіть!!!!!!)

Answer 1

Ответ:

Площадь восьмиугольника равна 48√2 ед.²

Ответ: Б)

Объяснение:

Правильный восьмиугольник вписан в окружность. Площадь кругового сектора, соответствующая центральному углу восьмиугольника, равна 3π. Найдите площадь восьмиугольника. Варианты ответов А) 6√2 ; Б) 48√2 ; В) 12√2; Г) 24√2.

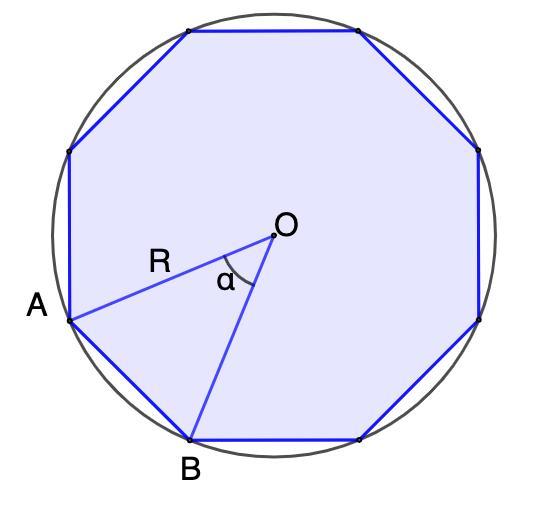
Дано: восьмиугольник;

Окр.(O; R) - описана около восьмиугольника;

α - центральный угол восьмиугольника.

Площадь кругового сектора, соответствующая углу α = 3π.

Найти: S восьмиугольника.

Решение:

• Центральный угол правильного многоугольника равен:
• α = 360° : n, где n - количество сторон многоугольника.

n = 8   ⇒  α = 360° : 8 = 45°

• Формула площади сектора:

• $\displaystyle S_{CEKT.}=\frac{\pi R^2\cdot \alpha ^0}{360^0}$

S сект. = 3π (условие); α = 45°.

Найдем радиус:

$\displaystyle 3\pi =\frac{\pi R^2\cdot 45^0}{360^0}\\ \\3\pi =\frac{\pi R^2}{8} \\\\R^2=24\\\\R=2\sqrt{6}$

• Площадь правильного многоугольника через радиус описанной окружности:

• $\displaystyle S=\frac{1}{2}R^2\cdot n \cdot sin\;\alpha$

Найдем площадь данного восьмиугольника:

$\displaystyle S=\frac{1}{2}\cdot 24\cdot 8\cdot sin\;45^0 =96\cdot \frac{\sqrt{2} }{2}=48\sqrt{2}$

Площадь восьмиугольника равна 48√2 ед.²

Ответ: Б)

#SPJ1